Menu Close

Let-x-1-x-2-x-3-be-the-roots-of-the-equation-x-3-3x-5-0-Then-the-value-of-expression-x-1-1-x-1-x-2-1-x-2-x-3-1-x-3-is-equal-to-

Tinku Tara 0 Comments
Pin




Question Number 162367 by cortano last updated on 29/Dec/21
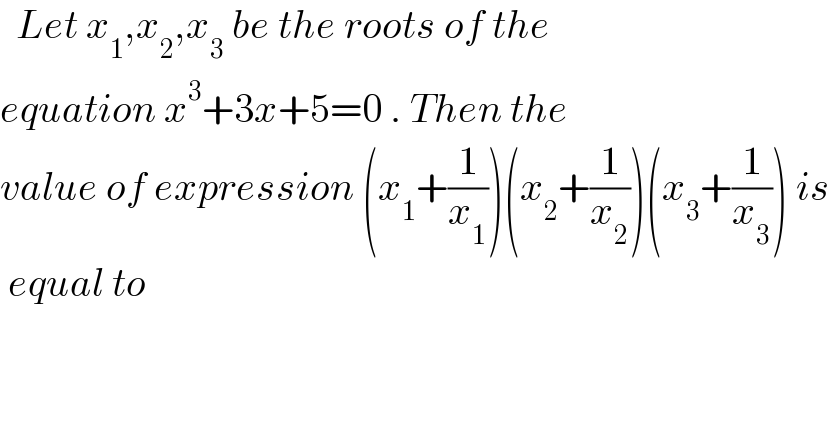
Let x_1 ,x_2 ,x_3 be the roots of the equation x^3 +3x+5=0 . Then the value of expression (x_1 +(1/x_1 ))(x_2 +(1/x_2 ))(x_3 +(1/x_3 )) is equal to
$$\:\:{Let}\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,{x}_{\mathrm{3}} \:{be}\:{the}\:{roots}\:{of}\:{the}\: \\ $$$${equation}\:{x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{5}=\mathrm{0}\:.\:{Then}\:{the} \\ $$$${value}\:{of}\:{expression}\:\left({x}_{\mathrm{1}} +\frac{\mathrm{1}}{{x}_{\mathrm{1}} }\right)\left({x}_{\mathrm{2}} +\frac{\mathrm{1}}{{x}_{\mathrm{2}} }\right)\left({x}_{\mathrm{3}} +\frac{\mathrm{1}}{{x}_{\mathrm{3}} }\right)\:{is} \\ $$$$\:{equal}\:{to} \\ $$
Answered by mr W last updated on 29/Dec/21
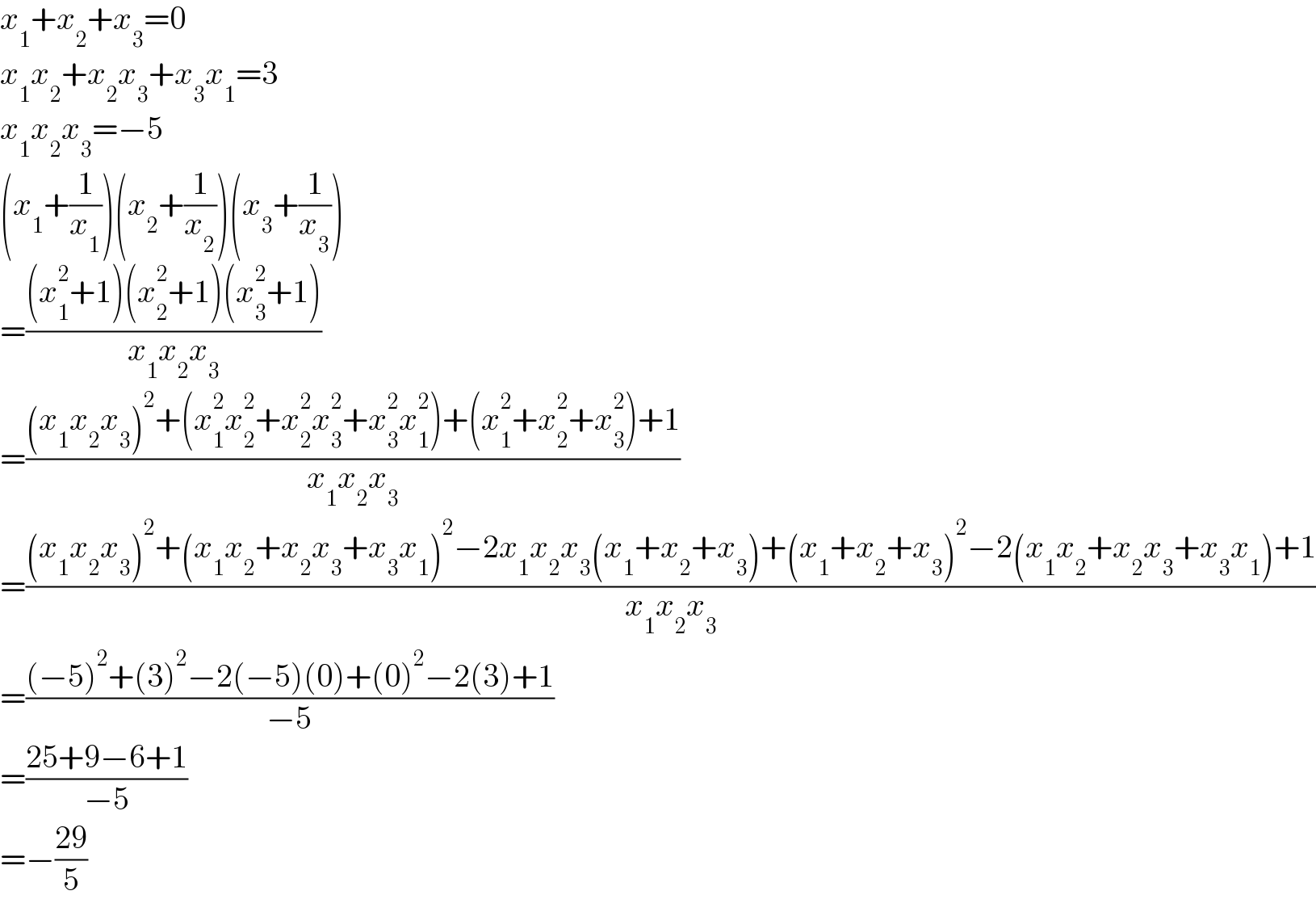
x_1 +x_2 +x_3 =0 x_1 x_2 +x_2 x_3 +x_3 x_1 =3 x_1 x_2 x_3 =−5 (x_1 +(1/x_1 ))(x_2 +(1/x_2 ))(x_3 +(1/x_3 )) =(((x_1 ^2 +1)(x_2 ^2 +1)(x_3 ^2 +1))/(x_1 x_2 x_3 )) =(((x_1 x_2 x_3 )^2 +(x_1 ^2 x_2 ^2 +x_2 ^2 x_3 ^2 +x_3 ^2 x_1 ^2 )+(x_1 ^2 +x_2 ^2 +x_3 ^2 )+1)/(x_1 x_2 x_3 )) =(((x_1 x_2 x_3 )^2 +(x_1 x_2 +x_2 x_3 +x_3 x_1 )^2 −2x_1 x_2 x_3 (x_1 +x_2 +x_3 )+(x_1 +x_2 +x_3 )^2 −2(x_1 x_2 +x_2 x_3 +x_3 x_1 )+1)/(x_1 x_2 x_3 )) =(((−5)^2 +(3)^2 −2(−5)(0)+(0)^2 −2(3)+1)/(−5)) =((25+9−6+1)/(−5)) =−((29)/5)
$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} =\mathrm{3} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} =−\mathrm{5} \\ $$$$\left({x}_{\mathrm{1}} +\frac{\mathrm{1}}{{x}_{\mathrm{1}} }\right)\left({x}_{\mathrm{2}} +\frac{\mathrm{1}}{{x}_{\mathrm{2}} }\right)\left({x}_{\mathrm{3}} +\frac{\mathrm{1}}{{x}_{\mathrm{3}} }\right) \\ $$$$=\frac{\left({x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}\right)\left({x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{1}\right)\left({x}_{\mathrm{3}} ^{\mathrm{2}} +\mathrm{1}\right)}{{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} } \\ $$$$=\frac{\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{1}} ^{\mathrm{2}} {x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} {x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} {x}_{\mathrm{1}} ^{\mathrm{2}} \right)+\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} \right)+\mathrm{1}}{{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} } \\ $$$$=\frac{\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} \left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right)+\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} \right)+\mathrm{1}}{{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} } \\ $$$$=\frac{\left(−\mathrm{5}\right)^{\mathrm{2}} +\left(\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{5}\right)\left(\mathrm{0}\right)+\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}\right)+\mathrm{1}}{−\mathrm{5}} \\ $$$$=\frac{\mathrm{25}+\mathrm{9}−\mathrm{6}+\mathrm{1}}{−\mathrm{5}} \\ $$$$=−\frac{\mathrm{29}}{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *