Question Number 54967 by gunawan last updated on 15/Feb/19
![Let x_1 , x_2 , x_3 the number real x_1 <x_2 <x_3 . T : P_2 →R^3 defined with rule T= [((P(x_1 ))),((P(x_2 ))),((P(x_3 ))) ] for all P(x) ∈ P_2 a) Prove that T form linear transformation b) check whether T bijektive](https://www.tinkutara.com/question/Q54967.png)
$$\mathrm{Let}\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} \:\mathrm{the}\:\mathrm{number}\:\mathrm{real} \\ $$$${x}_{\mathrm{1}} <{x}_{\mathrm{2}} <{x}_{\mathrm{3}} .\:{T}\::\:{P}_{\mathrm{2}} \rightarrow{R}^{\mathrm{3}} \:\mathrm{defined} \\ $$$$\mathrm{with}\:\mathrm{rule}\:{T}=\begin{bmatrix}{{P}\left({x}_{\mathrm{1}} \right)}\\{{P}\left({x}_{\mathrm{2}} \right)}\\{{P}\left({x}_{\mathrm{3}} \right)}\end{bmatrix} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{P}\left({x}\right)\:\in\:{P}_{\mathrm{2}} \\ $$$$\left.{a}\right)\:{P}\mathrm{rove}\:\mathrm{that}\:{T}\:\:\mathrm{form}\:\mathrm{linear}\:\mathrm{transformation} \\ $$$$\left.\mathrm{b}\right)\:\mathrm{check}\:\mathrm{whether}\:\:{T}\:\mathrm{bijektive} \\ $$
Commented by kaivan.ahmadi last updated on 15/Feb/19
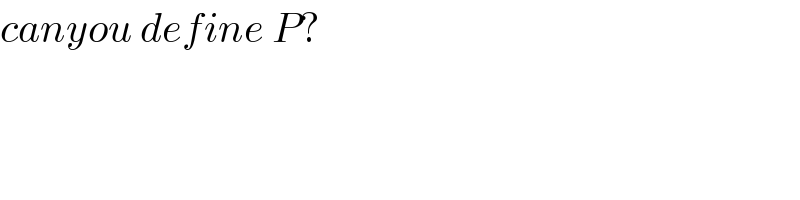
$${canyou}\:{define}\:{P}? \\ $$
Commented by gunawan last updated on 15/Feb/19

$${P}\:\:\mathrm{is}\:\mathrm{Polynomial} \\ $$
