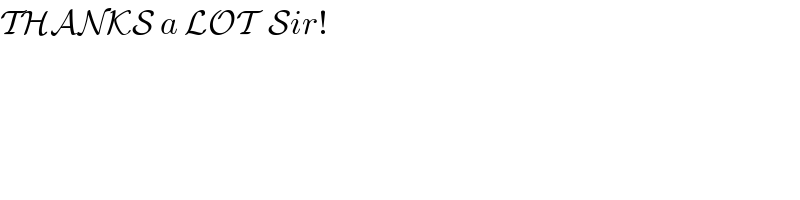Question Number 25230 by naka3546 last updated on 06/Dec/17
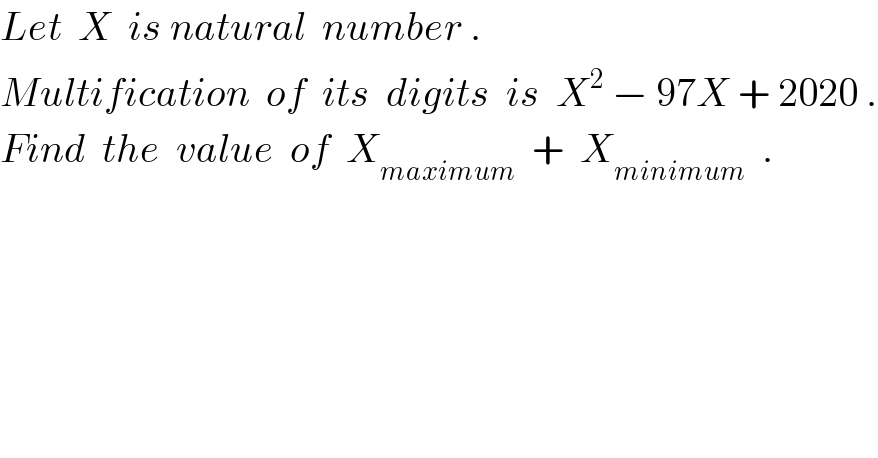
Answered by Rasheed.Sindhi last updated on 07/Dec/17
![Let X=(x_(n-1) x_(n-2) ...x_1 x_0 )_(10) , where x_(n-1) , x_(n-2) ,...,x_2 ,x_1 are decimal digits. X=x_(n-1) (10)^(n-1) +x_(n-2) (10)^(n-2) +...x_1 (10)^1 +x_0 x_(n-1) .x_(n-2) ...x_1 .x_0 =X^2 − 97X + 2020 An n-digit number_(max) =99...9^(n nines) So X^2 −97X+2020^(multiplication of digis) ≤9^n For 1-digit X^2 −97X+2020≤9 X≤66,X≤30⇒X≤66 The number is upto 2digit For 2-digit X^2 −97X+2020≤81 X≤28, X≤68⇒X≤68...(i) The number is upto 2digit. For 3-digit X^2 −97X+2020≤729 X≤15,X≤81⇒X≤81 The number cannot be 3digit. For 4-digit X^2 −97X+2020≤6561 X≤−34,X≤131⇒X≤131 The number cannot be 4digit. ...... .... .. It seems that the number cannot consist of more than 2-digit. If X is two digit number. Let the number is 10a+b ab=(10a+b)^2 −97(10a+b)+2020 ⇒100a^2 +19ab+b^2 −970a−97b+2020=0...(ii) Also from (i) 10a+b≤68⇒1≤a≤6 ∧ 0≤b≤8 a=1⇒ (ii)⇒100+19b+b^2 −970−97b+2020=0 b^2 −78b+1150=0 [No integer b] a=1,2,3,4,5 ⇒value of b is inadmissble But for a=6⇒ (ii)⇒3600+114b+b^2 −5820−97b+2020=0 b^2 +17b−200=0⇒b=8 Hence the single 2-digit number is 68 Verify that 6×8=68^2 −97(68)+2020 X_(max) +X_(min) =68+68=136](https://www.tinkutara.com/question/Q25232.png)
Commented by Rasheed.Sindhi last updated on 07/Dec/17

Commented by mrW1 last updated on 07/Dec/17
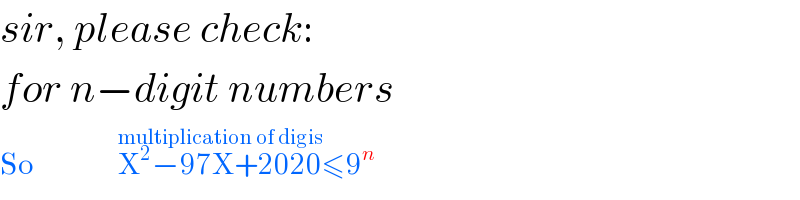
Commented by mrW1 last updated on 07/Dec/17

Commented by Rasheed.Sindhi last updated on 07/Dec/17