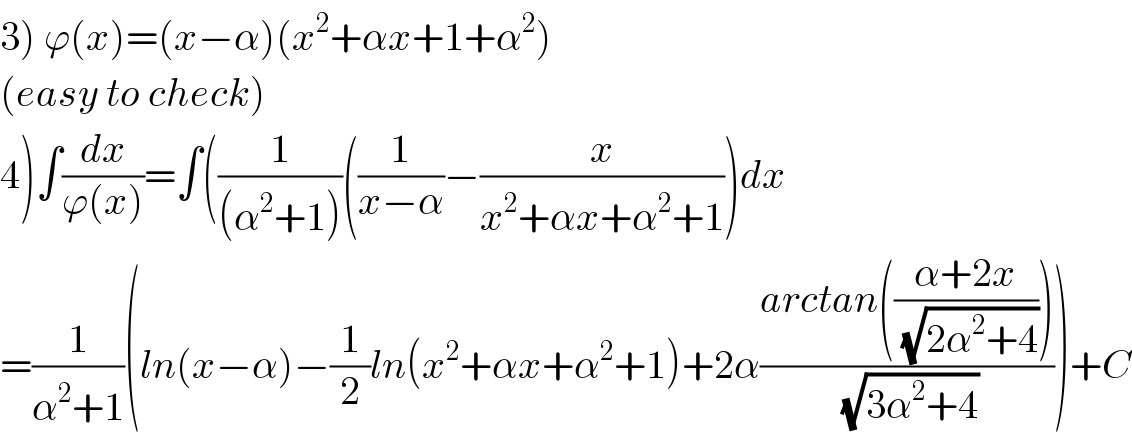let-x-x-3-x-1-1-prove-that-have-one-real-root-2-determine-a-approximate-value-for-by-use-of-newton-method-3-factorise-inside-R-x-f-x-4-calculste-dx-x-

Question Number 104772 by mathmax by abdo last updated on 23/Jul/20

let φ (x) = x^{3} + x + 1

1) prove that φ have one real root α

2) determine a approximate value for α by use of newton method

3) factorise inside R (x) f (x)

4) calculste \int \frac{dx}{φ (x)}

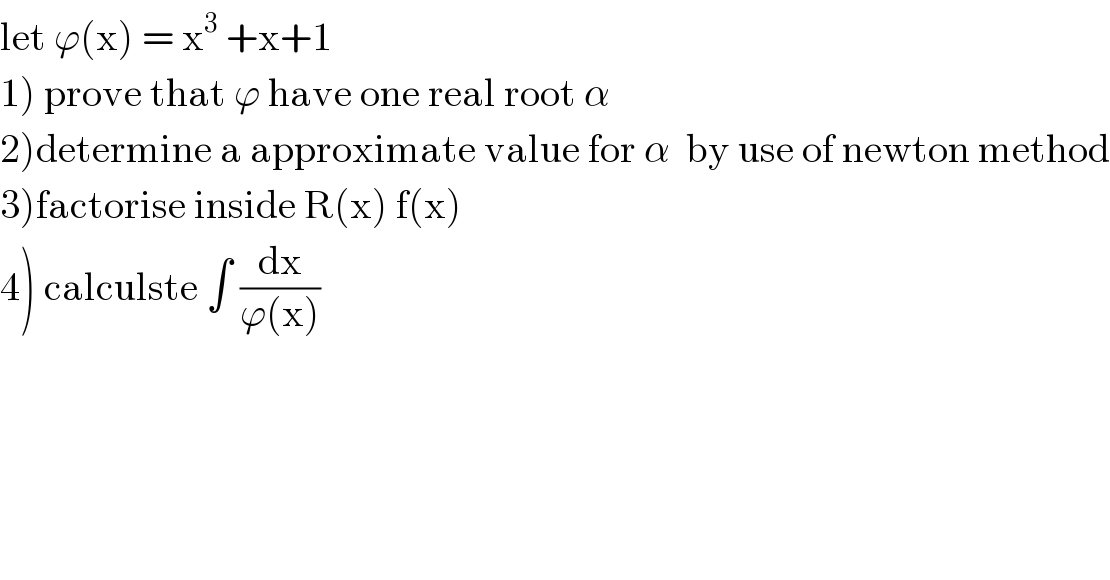
Answered by MAB last updated on 23/Jul/20

1) φ^{'} (x) = 3 x^{2} + 1 > 0

\lim_{x \to - \infty} φ (x) = - \infty

\lim_{x \to + \infty} φ (x) = + \infty

h e n c e φ i s a b i j e c t i o n o f] - \infty, + \infty [t o

i t s e l f, φ h a s a u n i q u e r e a l r o o t

2) x_{n + 1} = x_{n} - \frac{φ (x_{n})}{φ^{'} (x_{n})}

x_{n + 1} = x_{n} - \frac{x_{n}^{3} + x_{n} + 1}{3 x_{n}^{2} + 1}

x_{n + 1} = \frac{2 x_{n}^{3} - 1}{3 x_{n}^{2} - 1}

l e t x_{0} = 0

u s i n g p y t h o n x_{5} = - 0.6823278039465127

t o b e c o n t i n u e d \dots

Commented by abdomsup last updated on 23/Jul/20

t h a n k y o u s i r .

Commented by MAB last updated on 23/Jul/20

y o u a r e w e l c o m e s i r

Answered by MAB last updated on 23/Jul/20

3) φ (x) = (x - α) (x^{2} + α x + 1 + α^{2})

(e a s y t o c h e c k)

4) \int \frac{d x}{φ (x)} = \int (\frac{1}{(α^{2} + 1)} (\frac{1}{x - α} - \frac{x}{x^{2} + α x + α^{2} + 1}) d x

= \frac{1}{α^{2} + 1} (l n (x - α) - \frac{1}{2} l n (x^{2} + α x + α^{2} + 1) + 2 α \frac{a r c t a n (\frac{α + 2 x}{\sqrt{2 α^{2} + 4}})}{\sqrt{3 α^{2} + 4}}) + C

Facebook Tweet Pin