Question Number 182074 by Acem last updated on 04/Dec/22
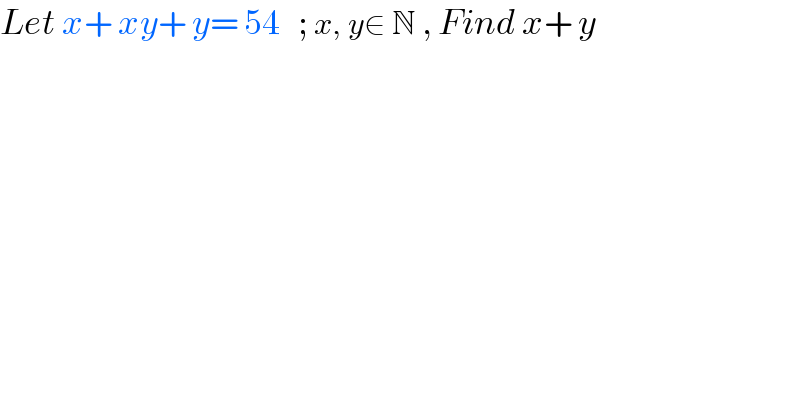
$${Let}\:{x}+\:{xy}+\:{y}=\:\mathrm{54}\:\:\:;\:{x},\:{y}\in\:\mathbb{N}\:,\:{Find}\:{x}+\:{y} \\ $$
Answered by HeferH last updated on 04/Dec/22
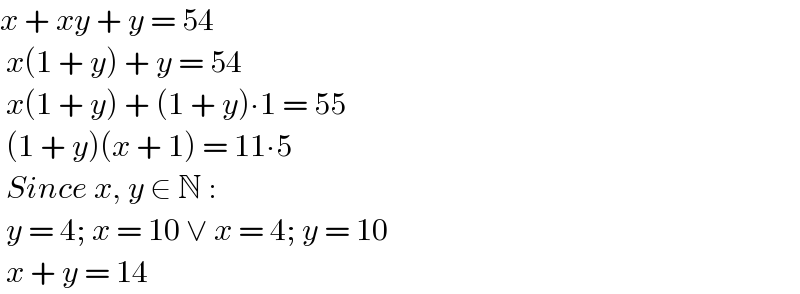
$${x}\:+\:{xy}\:+\:{y}\:=\:\mathrm{54} \\ $$$$\:{x}\left(\mathrm{1}\:+\:{y}\right)\:+\:{y}\:=\:\mathrm{54} \\ $$$$\:{x}\left(\mathrm{1}\:+\:{y}\right)\:+\:\left(\mathrm{1}\:+\:{y}\right)\centerdot\mathrm{1}\:=\:\mathrm{55} \\ $$$$\:\left(\mathrm{1}\:+\:{y}\right)\left({x}\:+\:\mathrm{1}\right)\:=\:\mathrm{11}\centerdot\mathrm{5} \\ $$$$\:{Since}\:{x},\:{y}\:\in\:\mathbb{N}\:: \\ $$$$\:{y}\:=\:\mathrm{4};\:{x}\:=\:\mathrm{10}\:\vee\:{x}\:=\:\mathrm{4};\:{y}\:=\:\mathrm{10}\: \\ $$$$\:{x}\:+\:{y}\:=\:\mathrm{14}\: \\ $$
Commented by Acem last updated on 04/Dec/22

$${Thanks}\:{Sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 04/Dec/22
![Let x+ xy+ y= 54 ; x, y∈ N , Find x+ y Another way x=((54−y)/(y+1))+1−1 x=((55)/(y+1))−1 y+1=1,5,11,55 [∵ x∈N⇒(y+1)∣55] y=0,4,10,54 x=54,10,4,0 (x,y)={(0,54),(4,10),(10,4),(54,0)} x+y=54,14 [54 in case 0∈N]](https://www.tinkutara.com/question/Q182086.png)
$${Let}\:{x}+\:{xy}+\:{y}=\:\mathrm{54}\:\:\:;\:{x},\:{y}\in\:\mathbb{N}\:,\:{Find}\:{x}+\:{y} \\ $$$$\mathbb{A}\mathrm{nother}\:\mathrm{way} \\ $$$$\:\:\:\:{x}=\frac{\mathrm{54}−{y}}{{y}+\mathrm{1}}+\mathrm{1}−\mathrm{1} \\ $$$$\:\:\:\:\:\:{x}=\frac{\mathrm{55}}{{y}+\mathrm{1}}−\mathrm{1} \\ $$$${y}+\mathrm{1}=\mathrm{1},\mathrm{5},\mathrm{11},\mathrm{55}\:\:\:\:\left[\because\:{x}\in\mathbb{N}\Rightarrow\left({y}+\mathrm{1}\right)\mid\mathrm{55}\right] \\ $$$${y}=\mathrm{0},\mathrm{4},\mathrm{10},\mathrm{54} \\ $$$${x}=\mathrm{54},\mathrm{10},\mathrm{4},\mathrm{0} \\ $$$$\left({x},{y}\right)=\left\{\left(\mathrm{0},\mathrm{54}\right),\left(\mathrm{4},\mathrm{10}\right),\left(\mathrm{10},\mathrm{4}\right),\left(\mathrm{54},\mathrm{0}\right)\right\} \\ $$$${x}+{y}=\mathrm{54},\mathrm{14} \\ $$$$\left[\mathrm{54}\:{in}\:{case}\:\mathrm{0}\in\mathbb{N}\right] \\ $$
Commented by Acem last updated on 04/Dec/22

$${Thanks}\:{Sir}! \\ $$
