Question Number 150903 by puissant last updated on 16/Aug/21

$${let}\:{x},{y}>\mathrm{0}\:,\:{n}\in\mathbb{N}, \\ $$$${show}\:{that}\:\left({x}+{y}\right)^{{n}} \leqslant\mathrm{2}^{{n}−\mathrm{1}} \left({x}^{{n}} +{y}^{{n}} \right).. \\ $$
Answered by qaz last updated on 16/Aug/21
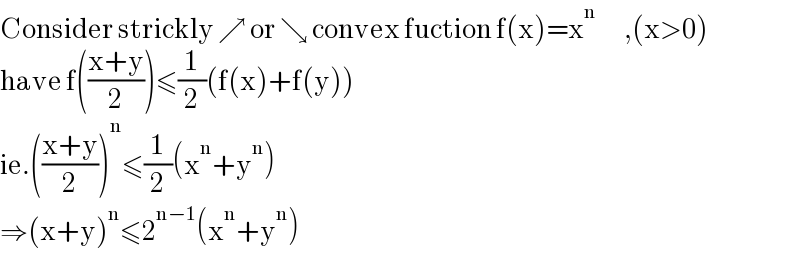
$$\mathrm{Consider}\:\mathrm{strickly}\:\nearrow\:\mathrm{or}\:\searrow\:\mathrm{convex}\:\mathrm{fuction}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{n}} \:\:\:\:\:\:\:,\left(\mathrm{x}>\mathrm{0}\right) \\ $$$$\mathrm{have}\:\mathrm{f}\left(\frac{\mathrm{x}+\mathrm{y}}{\mathrm{2}}\right)\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{y}\right)\right) \\ $$$$\mathrm{ie}.\left(\frac{\mathrm{x}+\mathrm{y}}{\mathrm{2}}\right)^{\mathrm{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{n}} +\mathrm{y}^{\mathrm{n}} \right) \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{n}} \leqslant\mathrm{2}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} +\mathrm{y}^{\mathrm{n}} \right) \\ $$
