Question Number 153381 by mathdanisur last updated on 06/Sep/21
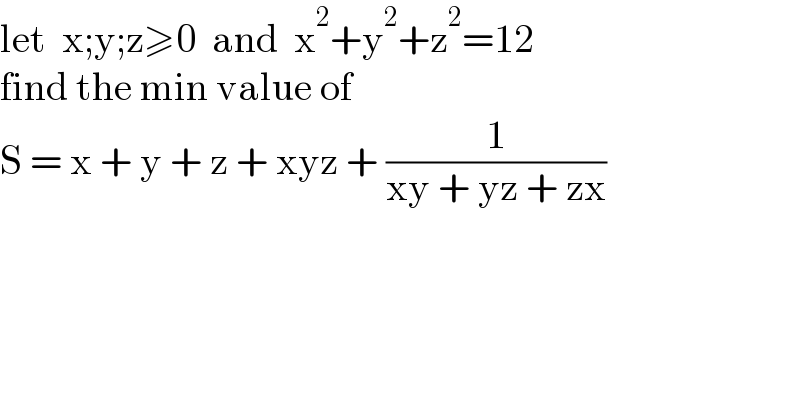
$$\mathrm{let}\:\:\mathrm{x};\mathrm{y};\mathrm{z}\geqslant\mathrm{0}\:\:\mathrm{and}\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{12} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{min}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{S}\:=\:\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:+\:\mathrm{xyz}\:+\:\frac{\mathrm{1}}{\mathrm{xy}\:+\:\mathrm{yz}\:+\:\mathrm{zx}} \\ $$
Commented by mr W last updated on 06/Sep/21
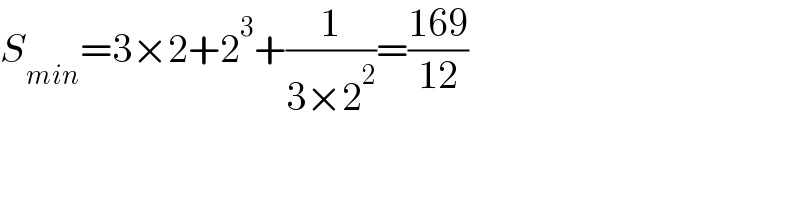
$${S}_{{min}} =\mathrm{3}×\mathrm{2}+\mathrm{2}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}×\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{169}}{\mathrm{12}} \\ $$
Commented by mathdanisur last updated on 07/Sep/21

$$\mathrm{No}\:\mathrm{ser}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$
