Question Number 107320 by pticantor last updated on 10/Aug/20
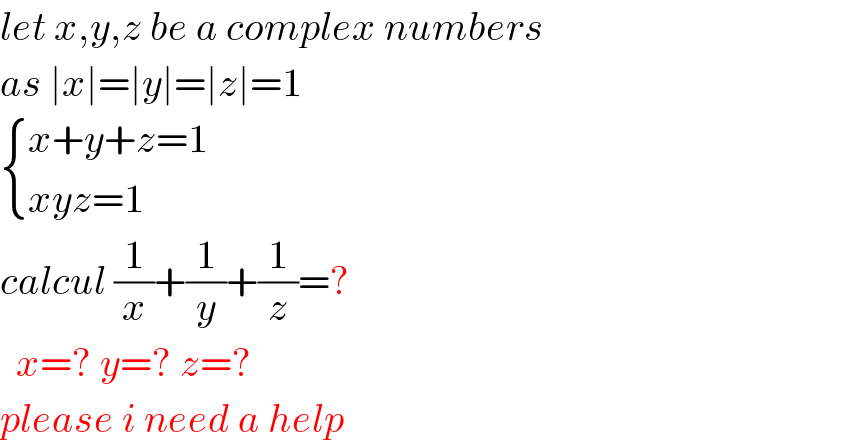
$${let}\:{x},{y},{z}\:{be}\:{a}\:{complex}\:{numbers} \\ $$$${as}\:\mid{x}\mid=\mid{y}\mid=\mid{z}\mid=\mathrm{1} \\ $$$$\begin{cases}{{x}+{y}+{z}=\mathrm{1}}\\{{xyz}=\mathrm{1}}\end{cases} \\ $$$${calcul}\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=? \\ $$$$\:\:{x}=?\:{y}=?\:{z}=? \\ $$$${please}\:{i}\:{need}\:{a}\:{help} \\ $$
Commented by bemath last updated on 10/Aug/20
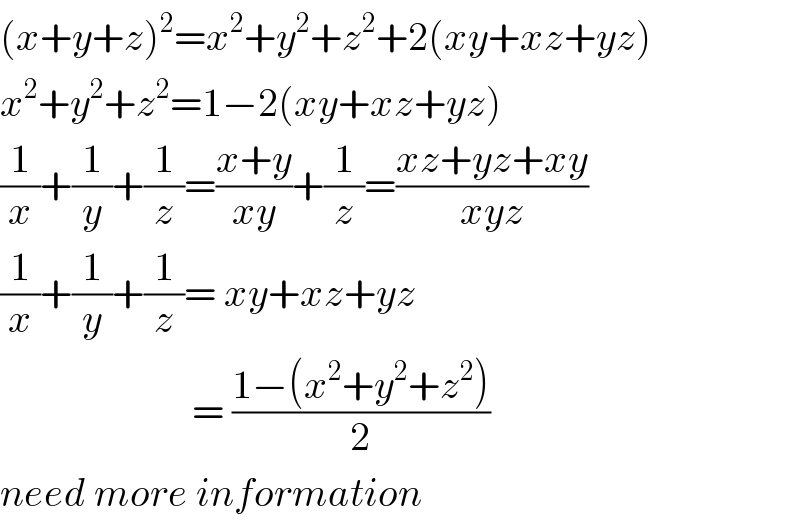
$$\left({x}+{y}+{z}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}\left({xy}+{xz}+{yz}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}\left({xy}+{xz}+{yz}\right) \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{{x}+{y}}{{xy}}+\frac{\mathrm{1}}{{z}}=\frac{{xz}+{yz}+{xy}}{{xyz}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\:{xy}+{xz}+{yz} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$${need}\:{more}\:{information} \\ $$
Commented by pticantor last updated on 10/Aug/20
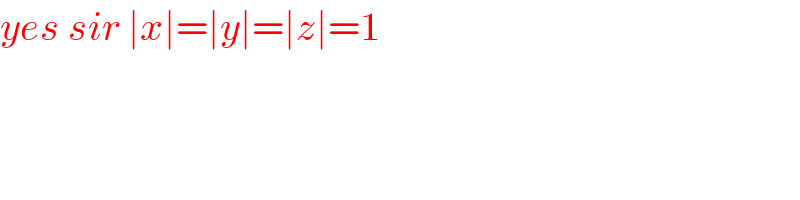
$${yes}\:{sir}\:\mid{x}\mid=\mid{y}\mid=\mid{z}\mid=\mathrm{1} \\ $$
Commented by bemath last updated on 10/Aug/20
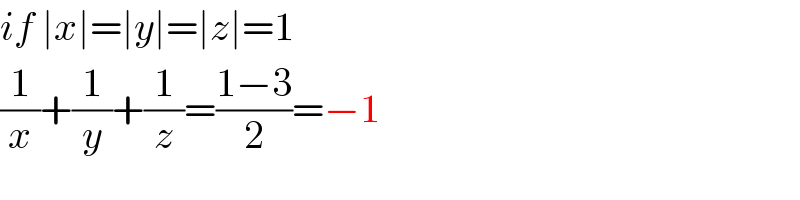
$${if}\:\mid{x}\mid=\mid{y}\mid=\mid{z}\mid=\mathrm{1}\: \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}−\mathrm{3}}{\mathrm{2}}=−\mathrm{1} \\ $$
Commented by pticantor last updated on 10/Aug/20

$${how}\:{sir}\:??? \\ $$$${we}\:{have}\:{x}^{\mathrm{2}} #\:\mid{x}\mid \\ $$
Commented by bemath last updated on 10/Aug/20
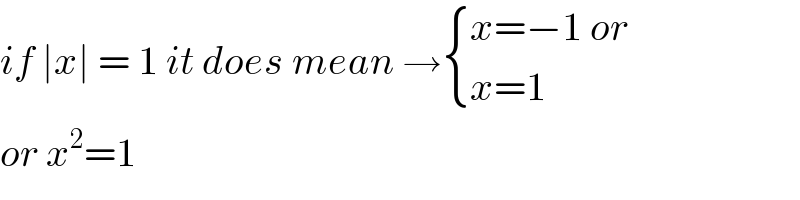
$${if}\:\mid{x}\mid\:=\:\mathrm{1}\:{it}\:{does}\:{mean}\:\rightarrow\begin{cases}{{x}=−\mathrm{1}\:{or}}\\{{x}=\mathrm{1}}\end{cases} \\ $$$${or}\:{x}^{\mathrm{2}} =\mathrm{1} \\ $$
Commented by Her_Majesty last updated on 10/Aug/20
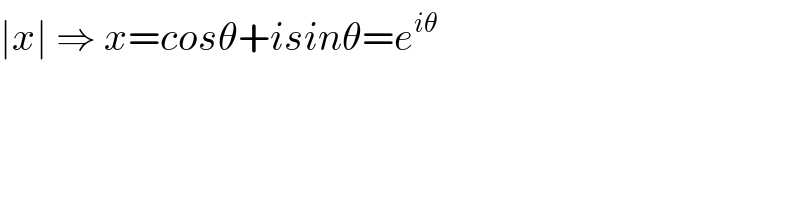
$$\mid{x}\mid\:\Rightarrow\:{x}={cos}\theta+{isin}\theta={e}^{{i}\theta} \\ $$
Answered by Her_Majesty last updated on 10/Aug/20
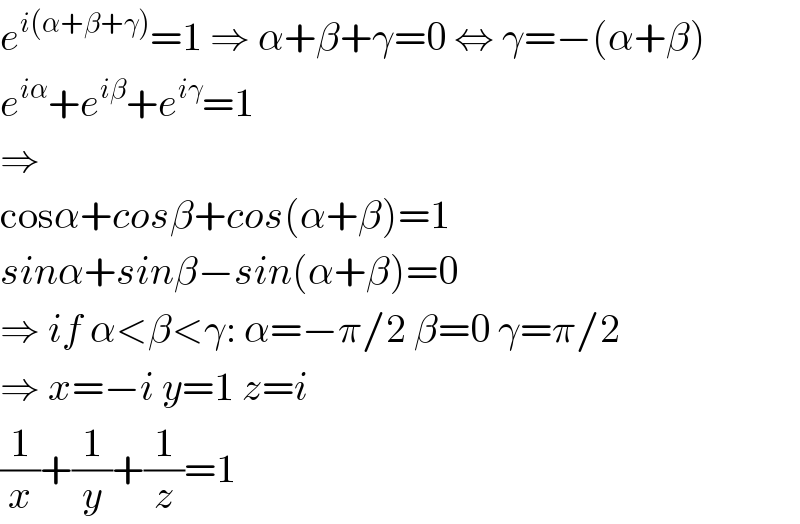
$${e}^{{i}\left(\alpha+\beta+\gamma\right)} =\mathrm{1}\:\Rightarrow\:\alpha+\beta+\gamma=\mathrm{0}\:\Leftrightarrow\:\gamma=−\left(\alpha+\beta\right) \\ $$$${e}^{{i}\alpha} +{e}^{{i}\beta} +{e}^{{i}\gamma} =\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{cos}\alpha+{cos}\beta+{cos}\left(\alpha+\beta\right)=\mathrm{1} \\ $$$${sin}\alpha+{sin}\beta−{sin}\left(\alpha+\beta\right)=\mathrm{0} \\ $$$$\Rightarrow\:{if}\:\alpha<\beta<\gamma:\:\alpha=−\pi/\mathrm{2}\:\beta=\mathrm{0}\:\gamma=\pi/\mathrm{2} \\ $$$$\Rightarrow\:{x}=−{i}\:{y}=\mathrm{1}\:{z}={i} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\mathrm{1} \\ $$
Commented by bemath last updated on 10/Aug/20
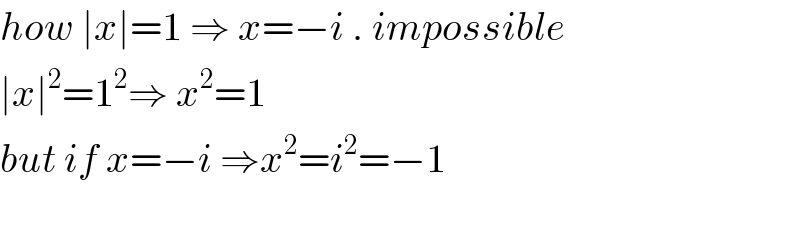
$${how}\:\mid{x}\mid=\mathrm{1}\:\Rightarrow\:{x}=−{i}\:.\:{impossible} \\ $$$$\mid{x}\mid^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \Rightarrow\:{x}^{\mathrm{2}} =\mathrm{1} \\ $$$${but}\:{if}\:{x}=−{i}\:\Rightarrow{x}^{\mathrm{2}} ={i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$
Commented by Her_Majesty last updated on 10/Aug/20
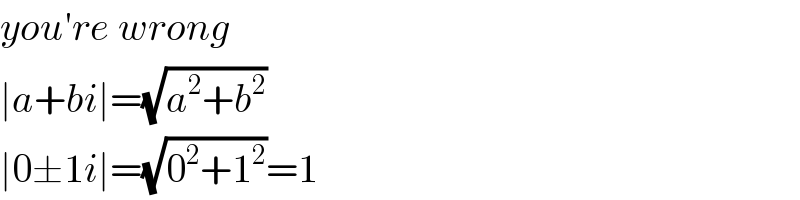
$${you}'{re}\:{wrong} \\ $$$$\mid{a}+{bi}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mid\mathrm{0}\pm\mathrm{1}{i}\mid=\sqrt{\mathrm{0}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\mathrm{1} \\ $$
Commented by Her_Majesty last updated on 10/Aug/20

$${who}\:{marked}\:{this}\:{as}\:{inappropriate}? \\ $$$${the}\:{question}\:{says}\:“{x}\:{y}\:{z}\:{are}\:{complex}\:{numbers}'' \\ $$$${z}={re}^{{i}\theta} ={rcos}\theta+{irsin}\theta={a}+{bi}\:{with}\:{r}\in\mathbb{R}^{+} \\ $$$$\mid{z}\mid={r}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${if}\:{you}\:{do}\:{not}\:{know}\:{this},\:{learn}\:{it}\:{right}\:{now}! \\ $$
Commented by bemath last updated on 10/Aug/20
wow .... I don't know who did that action.
