Menu Close

Let-x-y-z-be-non-negative-real-numbers-such-that-x-y-z-1-Find-the-extremum-of-F-2x-2-y-3z-2-

Tinku Tara 0 Comments
Pin




Question Number 119724 by benjo_mathlover last updated on 26/Oct/20
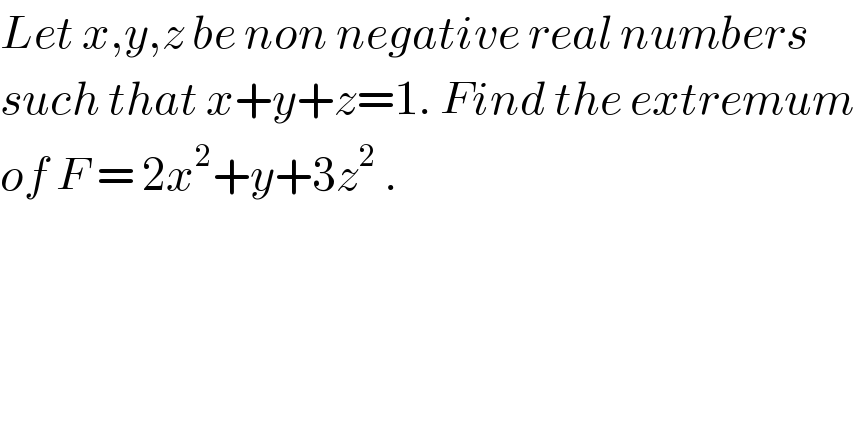
Let x,y,z be non negative real numbers such that x+y+z=1. Find the extremum of F = 2x^2 +y+3z^2 .
$${Let}\:{x},{y},{z}\:{be}\:{non}\:{negative}\:{real}\:{numbers} \\ $$$${such}\:{that}\:{x}+{y}+{z}=\mathrm{1}.\:{Find}\:{the}\:{extremum} \\ $$$${of}\:{F}\:=\:\mathrm{2}{x}^{\mathrm{2}} +{y}+\mathrm{3}{z}^{\mathrm{2}} \:. \\ $$
Answered by mindispower last updated on 26/Oct/20
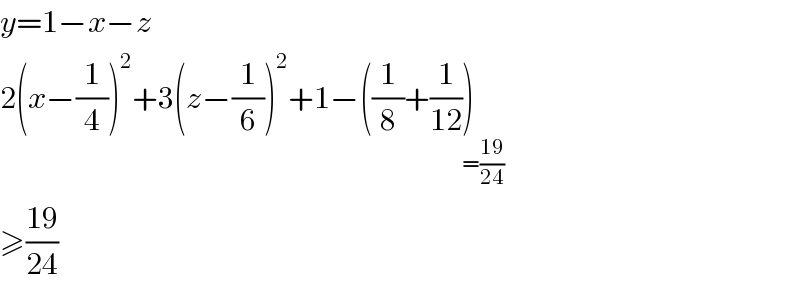
y=1−x−z 2(x−(1/4))^2 +3(z−(1/6))^2 +1−((1/8)+(1/(12)))_(=((19)/(24))) ≥((19)/(24))
$${y}=\mathrm{1}−{x}−{z} \\ $$$$\mathrm{2}\left({x}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{3}\left({z}−\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{12}}\underset{=\frac{\mathrm{19}}{\mathrm{24}}} {\right)} \\ $$$$\geqslant\frac{\mathrm{19}}{\mathrm{24}} \\ $$
Commented by bemath last updated on 26/Oct/20
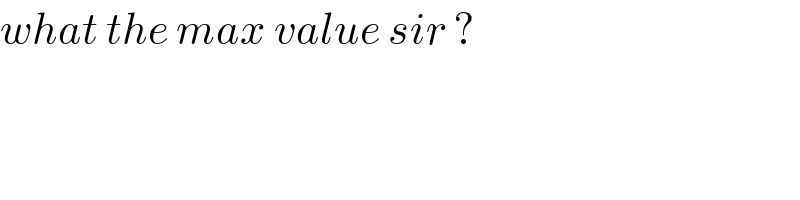
what the max value sir ?
$${what}\:{the}\:{max}\:{value}\:{sir}\:? \\ $$
Answered by 1549442205PVT last updated on 27/Oct/20
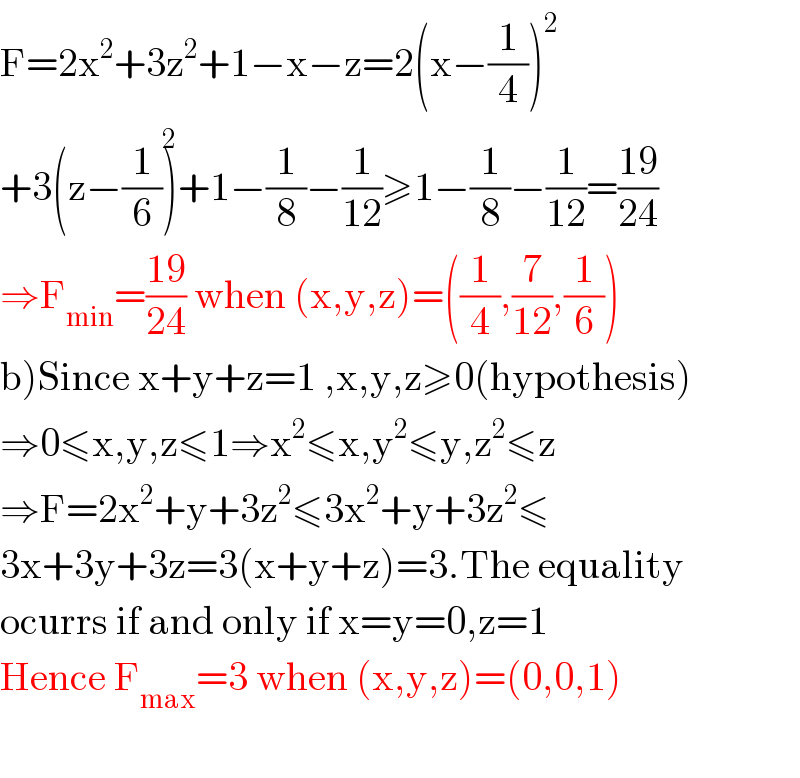
F=2x^2 +3z^2 +1−x−z=2(x−(1/4))^2 +3(z−(1/6))^2 +1−(1/8)−(1/(12))≥1−(1/8)−(1/(12))=((19)/(24)) ⇒F_(min) =((19)/(24)) when (x,y,z)=((1/4),(7/(12)),(1/6)) b)Since x+y+z=1 ,x,y,z≥0(hypothesis) ⇒0≤x,y,z≤1⇒x^2 ≤x,y^2 ≤y,z^2 ≤z ⇒F=2x^2 +y+3z^2 ≤3x^2 +y+3z^2 ≤ 3x+3y+3z=3(x+y+z)=3.The equality ocurrs if and only if x=y=0,z=1 Hence F_(max) =3 when (x,y,z)=(0,0,1)
$$\mathrm{F}=\mathrm{2x}^{\mathrm{2}} +\mathrm{3z}^{\mathrm{2}} +\mathrm{1}−\mathrm{x}−\mathrm{z}=\mathrm{2}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$+\mathrm{3}\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{6}}\overset{\mathrm{2}} {\right)}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{12}}\geqslant\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{19}}{\mathrm{24}} \\ $$$$\Rightarrow\mathrm{F}_{\mathrm{min}} =\frac{\mathrm{19}}{\mathrm{24}}\:\mathrm{when}\:\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{7}}{\mathrm{12}},\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$\left.\mathrm{b}\right)\mathrm{Since}\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1}\:,\mathrm{x},\mathrm{y},\mathrm{z}\geqslant\mathrm{0}\left(\mathrm{hypothesis}\right) \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{x},\mathrm{y},\mathrm{z}\leqslant\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} \leqslant\mathrm{x},\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{y},\mathrm{z}^{\mathrm{2}} \leqslant\mathrm{z} \\ $$$$\Rightarrow\mathrm{F}=\mathrm{2x}^{\mathrm{2}} +\mathrm{y}+\mathrm{3z}^{\mathrm{2}} \leqslant\mathrm{3x}^{\mathrm{2}} +\mathrm{y}+\mathrm{3z}^{\mathrm{2}} \leqslant \\ $$$$\mathrm{3x}+\mathrm{3y}+\mathrm{3z}=\mathrm{3}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=\mathrm{3}.\mathrm{The}\:\mathrm{equality} \\ $$$$\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{x}=\mathrm{y}=\mathrm{0},\mathrm{z}=\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{F}_{\mathrm{max}} =\mathrm{3}\:\mathrm{when}\:\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{1}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *