Question Number 162788 by HongKing last updated on 01/Jan/22
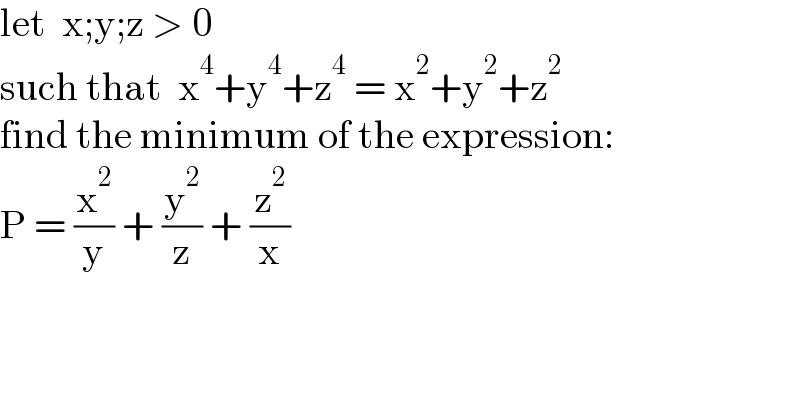
$$\mathrm{let}\:\:\mathrm{x};\mathrm{y};\mathrm{z}\:>\:\mathrm{0} \\ $$$$\mathrm{such}\:\mathrm{that}\:\:\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} +\mathrm{z}^{\mathrm{4}} \:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression}: \\ $$$$\mathrm{P}\:=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}}\:+\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{z}}\:+\:\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{x}} \\ $$
Answered by alephzero last updated on 01/Jan/22
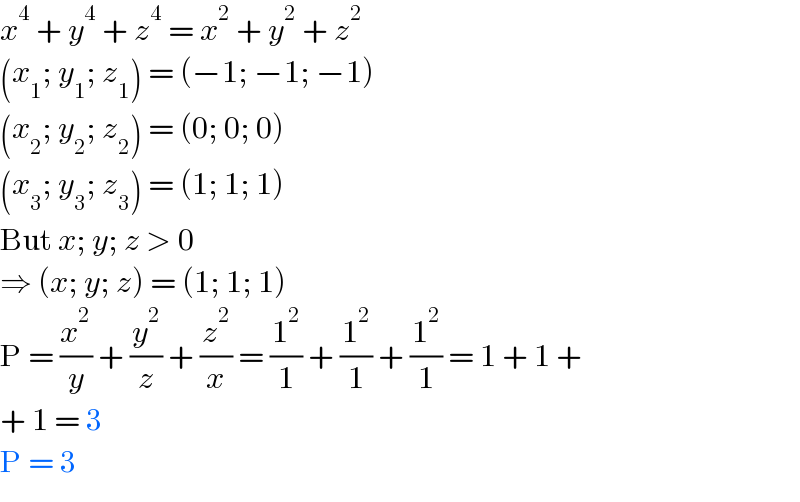
$${x}^{\mathrm{4}} \:+\:{y}^{\mathrm{4}} \:+\:{z}^{\mathrm{4}} \:=\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{1}} ;\:{y}_{\mathrm{1}} ;\:{z}_{\mathrm{1}} \right)\:=\:\left(−\mathrm{1};\:−\mathrm{1};\:−\mathrm{1}\right) \\ $$$$\left({x}_{\mathrm{2}} ;\:{y}_{\mathrm{2}} ;\:{z}_{\mathrm{2}} \right)\:=\:\left(\mathrm{0};\:\mathrm{0};\:\mathrm{0}\right) \\ $$$$\left({x}_{\mathrm{3}} ;\:{y}_{\mathrm{3}} ;\:{z}_{\mathrm{3}} \right)\:=\:\left(\mathrm{1};\:\mathrm{1};\:\mathrm{1}\right) \\ $$$$\mathrm{But}\:{x};\:{y};\:{z}\:>\:\mathrm{0} \\ $$$$\Rightarrow\:\left({x};\:{y};\:{z}\right)\:=\:\left(\mathrm{1};\:\mathrm{1};\:\mathrm{1}\right) \\ $$$$\mathrm{P}\:=\:\frac{{x}^{\mathrm{2}} }{{y}}\:+\:\frac{{y}^{\mathrm{2}} }{{z}}\:+\:\frac{{z}^{\mathrm{2}} }{{x}}\:=\:\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}}\:+\:\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}}\:+\:\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}}\:=\:\mathrm{1}\:+\:\mathrm{1}\:+ \\ $$$$+\:\mathrm{1}\:=\:\mathrm{3} \\ $$$$\mathrm{P}\:=\:\mathrm{3} \\ $$
Commented by HongKing last updated on 01/Jan/22
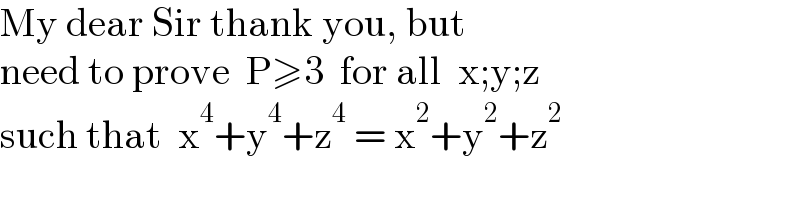
$$\mathrm{My}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you},\:\mathrm{but} \\ $$$$\mathrm{need}\:\mathrm{to}\:\mathrm{prove}\:\:\mathrm{P}\geqslant\mathrm{3}\:\:\mathrm{for}\:\mathrm{all}\:\:\mathrm{x};\mathrm{y};\mathrm{z} \\ $$$$\mathrm{such}\:\mathrm{that}\:\:\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} +\mathrm{z}^{\mathrm{4}} \:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \\ $$
