Menu Close

Let-x-y-Z-if-x-2-y-2-divide-xy-1-then-prove-x-2-y-2-xy-1-is-square-of-integer-number-

Tinku Tara 0 Comments
Pin




Question Number 53618 by kaivan.ahmadi last updated on 23/Jan/19
Let x,y∈Z if x^2 +y^2 divide xy+1 then prove ((x^2 +y^2 )/(xy+1)) is square of integer number
$$\mathrm{Let}\:\mathrm{x},\mathrm{y}\in\mathbb{Z} \\ $$$$\mathrm{if}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:\mathrm{divide}\:\mathrm{xy}+\mathrm{1}\:\mathrm{then}\:\mathrm{prove} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}+\mathrm{1}}\:\mathrm{is}\:\mathrm{square}\:\mathrm{of}\:\mathrm{integer}\:\mathrm{number} \\ $$
Commented by mr W last updated on 24/Jan/19
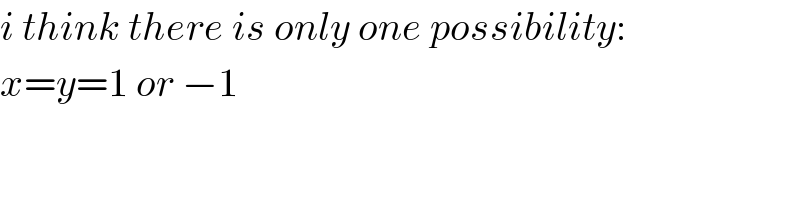
i think there is only one possibility: x=y=1 or −1
$${i}\:{think}\:{there}\:{is}\:{only}\:{one}\:{possibility}: \\ $$$${x}={y}=\mathrm{1}\:{or}\:−\mathrm{1} \\ $$
Commented by kaivan.ahmadi last updated on 24/Jan/19
thank you, chek the proof....
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{chek}\:\mathrm{the}\:\mathrm{proof}…. \\ $$
Commented by Kunal12588 last updated on 28/Mar/19
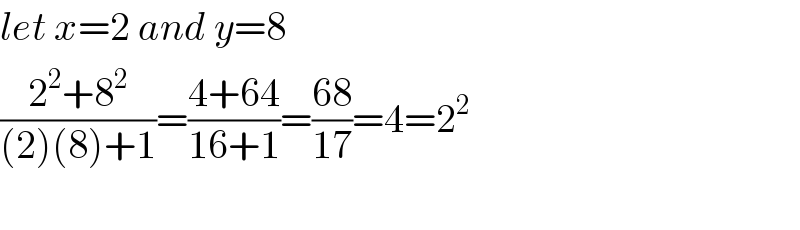
let x=2 and y=8 ((2^2 +8^2 )/((2)(8)+1))=((4+64)/(16+1))=((68)/(17))=4=2^2
$${let}\:{x}=\mathrm{2}\:{and}\:{y}=\mathrm{8} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }{\left(\mathrm{2}\right)\left(\mathrm{8}\right)+\mathrm{1}}=\frac{\mathrm{4}+\mathrm{64}}{\mathrm{16}+\mathrm{1}}=\frac{\mathrm{68}}{\mathrm{17}}=\mathrm{4}=\mathrm{2}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by kaivan.ahmadi last updated on 24/Jan/19
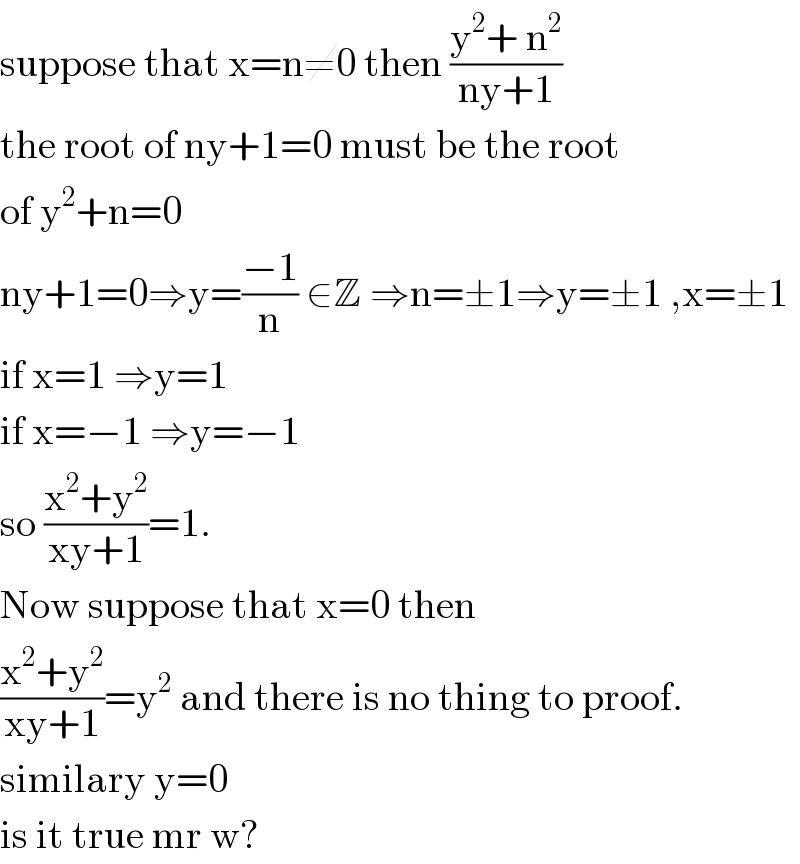
suppose that x=n≠0 then ((y^2 + n^2 )/(ny+1)) the root of ny+1=0 must be the root of y^2 +n=0 ny+1=0⇒y=((−1)/n) ∈Z ⇒n=±1⇒y=±1 ,x=±1 if x=1 ⇒y=1 if x=−1 ⇒y=−1 so ((x^2 +y^2 )/(xy+1))=1. Now suppose that x=0 then ((x^2 +y^2 )/(xy+1))=y^2 and there is no thing to proof. similary y=0 is it true mr w?
$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{x}=\mathrm{n}\neq\mathrm{0}\:\mathrm{then}\:\frac{\mathrm{y}^{\mathrm{2}} +\:\mathrm{n}^{\mathrm{2}} }{\mathrm{ny}+\mathrm{1}} \\ $$$$\mathrm{the}\:\mathrm{root}\:\mathrm{of}\:\mathrm{ny}+\mathrm{1}=\mathrm{0}\:\mathrm{must}\:\mathrm{be}\:\mathrm{the}\:\mathrm{root} \\ $$$$\mathrm{of}\:\mathrm{y}^{\mathrm{2}} +\mathrm{n}=\mathrm{0} \\ $$$$\mathrm{ny}+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{y}=\frac{−\mathrm{1}}{\mathrm{n}}\:\in\mathbb{Z}\:\Rightarrow\mathrm{n}=\pm\mathrm{1}\Rightarrow\mathrm{y}=\pm\mathrm{1}\:,\mathrm{x}=\pm\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{1}\:\Rightarrow\mathrm{y}=\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{x}=−\mathrm{1}\:\Rightarrow\mathrm{y}=−\mathrm{1} \\ $$$$\mathrm{so}\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}+\mathrm{1}}=\mathrm{1}. \\ $$$$\mathrm{Now}\:\mathrm{suppose}\:\mathrm{that}\:\mathrm{x}=\mathrm{0}\:\mathrm{then} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}+\mathrm{1}}=\mathrm{y}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{thing}\:\mathrm{to}\:\mathrm{proof}. \\ $$$$\mathrm{similary}\:\mathrm{y}=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{true}\:\mathrm{mr}\:\mathrm{w}? \\ $$
Commented by mr W last updated on 24/Jan/19
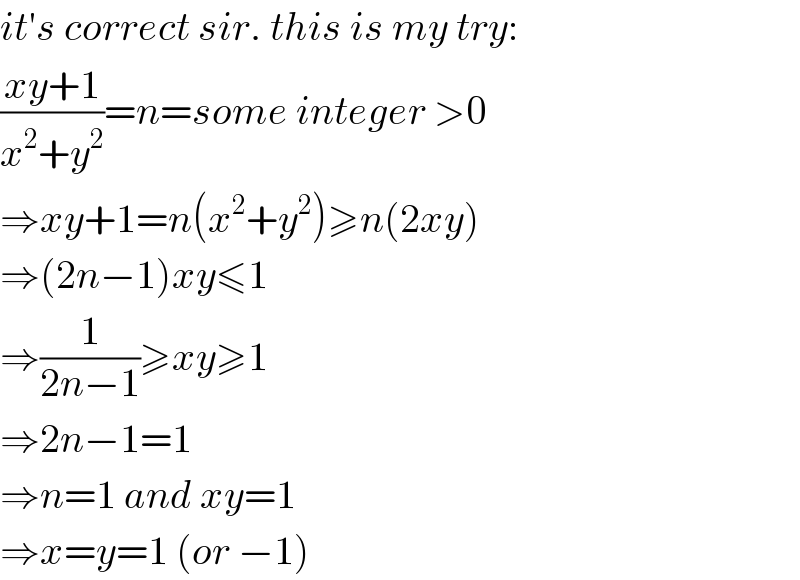
it′s correct sir. this is my try: ((xy+1)/(x^2 +y^2 ))=n=some integer >0 ⇒xy+1=n(x^2 +y^2 )≥n(2xy) ⇒(2n−1)xy≤1 ⇒(1/(2n−1))≥xy≥1 ⇒2n−1=1 ⇒n=1 and xy=1 ⇒x=y=1 (or −1)
$${it}'{s}\:{correct}\:{sir}.\:{this}\:{is}\:{my}\:{try}: \\ $$$$\frac{{xy}+\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }={n}={some}\:{integer}\:>\mathrm{0} \\ $$$$\Rightarrow{xy}+\mathrm{1}={n}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\geqslant{n}\left(\mathrm{2}{xy}\right) \\ $$$$\Rightarrow\left(\mathrm{2}{n}−\mathrm{1}\right){xy}\leqslant\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\geqslant{xy}\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{n}−\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow{n}=\mathrm{1}\:{and}\:{xy}=\mathrm{1} \\ $$$$\Rightarrow{x}={y}=\mathrm{1}\:\left({or}\:−\mathrm{1}\right) \\ $$
Commented by kaivan.ahmadi last updated on 24/Jan/19
very nice.attaching x=0 or y=0 complete the proof. thank you sir.
$$\mathrm{very}\:\mathrm{nice}.\mathrm{attaching}\:\:\mathrm{x}=\mathrm{0}\:\mathrm{or}\:\mathrm{y}=\mathrm{0}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{proof}. \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *