Question Number 52498 by Joel578 last updated on 09/Jan/19
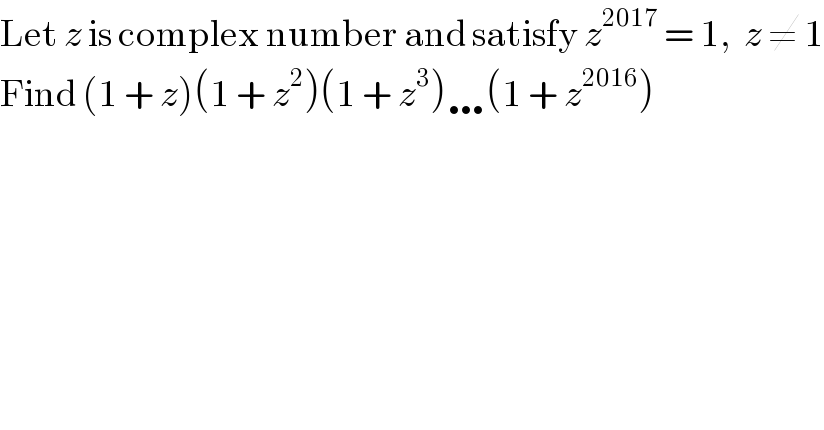
$$\mathrm{Let}\:{z}\:\mathrm{is}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{and}\:\mathrm{satisfy}\:{z}^{\mathrm{2017}} \:=\:\mathrm{1},\:\:{z}\:\neq\:\mathrm{1} \\ $$$$\mathrm{Find}\:\left(\mathrm{1}\:+\:{z}\right)\left(\mathrm{1}\:+\:{z}^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:{z}^{\mathrm{3}} \right)\ldots\left(\mathrm{1}\:+\:{z}^{\mathrm{2016}} \right) \\ $$
Commented by mr W last updated on 09/Jan/19
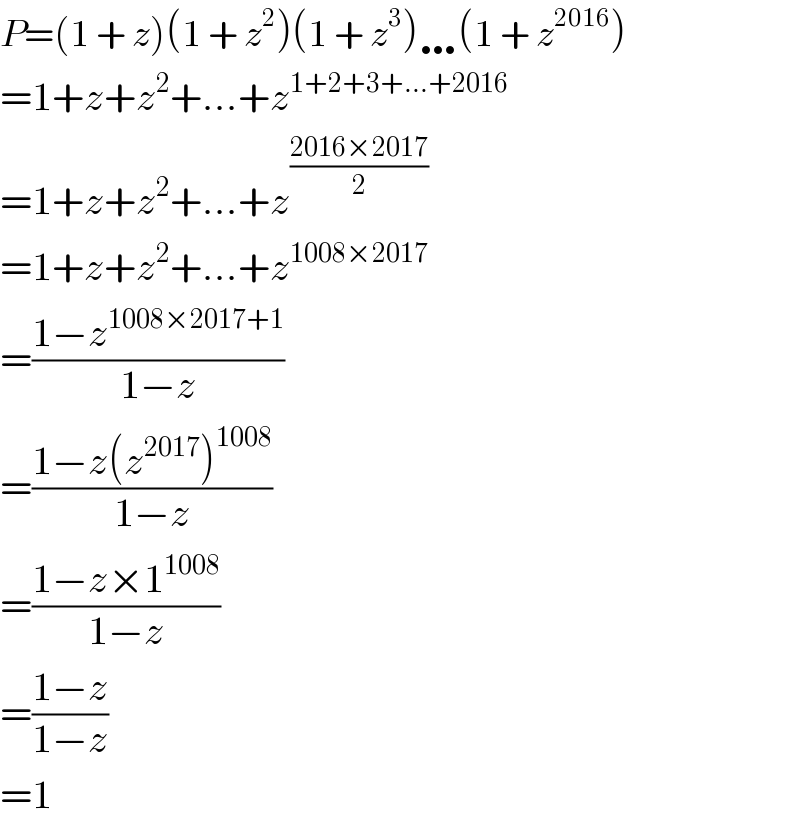
$${P}=\left(\mathrm{1}\:+\:{z}\right)\left(\mathrm{1}\:+\:{z}^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:{z}^{\mathrm{3}} \right)\ldots\left(\mathrm{1}\:+\:{z}^{\mathrm{2016}} \right) \\ $$$$=\mathrm{1}+{z}+{z}^{\mathrm{2}} +…+{z}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{2016}} \\ $$$$=\mathrm{1}+{z}+{z}^{\mathrm{2}} +…+{z}^{\frac{\mathrm{2016}×\mathrm{2017}}{\mathrm{2}}} \\ $$$$=\mathrm{1}+{z}+{z}^{\mathrm{2}} +…+{z}^{\mathrm{1008}×\mathrm{2017}} \\ $$$$=\frac{\mathrm{1}−{z}^{\mathrm{1008}×\mathrm{2017}+\mathrm{1}} }{\mathrm{1}−{z}} \\ $$$$=\frac{\mathrm{1}−{z}\left({z}^{\mathrm{2017}} \right)^{\mathrm{1008}} }{\mathrm{1}−{z}} \\ $$$$=\frac{\mathrm{1}−{z}×\mathrm{1}^{\mathrm{1008}} }{\mathrm{1}−{z}} \\ $$$$=\frac{\mathrm{1}−{z}}{\mathrm{1}−{z}} \\ $$$$=\mathrm{1} \\ $$
Answered by MJS last updated on 09/Jan/19
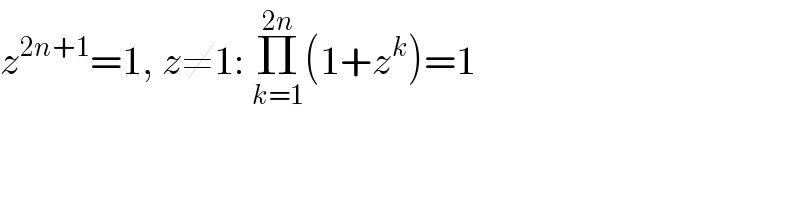
$${z}^{\mathrm{2}{n}+\mathrm{1}} =\mathrm{1},\:{z}\neq\mathrm{1}:\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\prod}}\left(\mathrm{1}+{z}^{{k}} \right)=\mathrm{1} \\ $$
Commented by malwaan last updated on 10/Jan/19

$$\mathrm{how}? \\ $$
