Question Number 146311 by mathdanisur last updated on 12/Jul/21
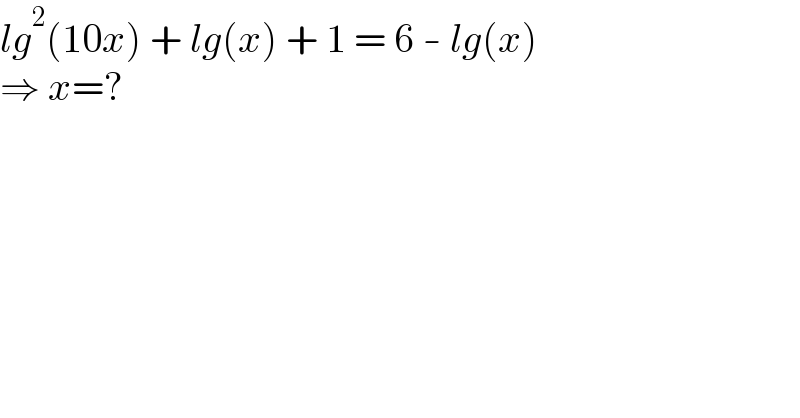
$${lg}^{\mathrm{2}} \left(\mathrm{10}{x}\right)\:+\:{lg}\left({x}\right)\:+\:\mathrm{1}\:=\:\mathrm{6}\:-\:{lg}\left({x}\right) \\ $$$$\Rightarrow\:{x}=? \\ $$
Commented by iloveisrael last updated on 13/Jul/21
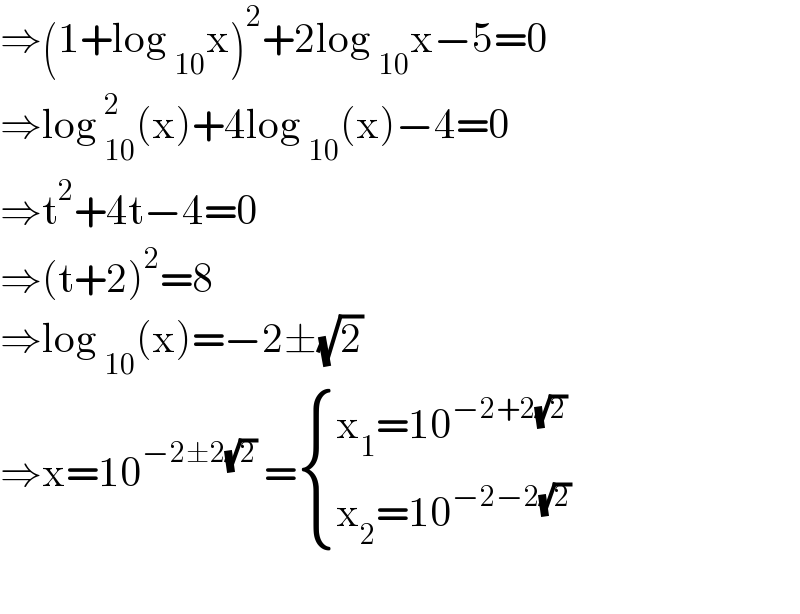
$$\Rightarrow\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{10}} \mathrm{x}\right)^{\mathrm{2}} +\mathrm{2log}\:_{\mathrm{10}} \mathrm{x}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{10}} ^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{4log}\:_{\mathrm{10}} \left(\mathrm{x}\right)−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{2}} +\mathrm{4t}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{8} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{x}\right)=−\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{10}^{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{2}}} \:=\begin{cases}{\mathrm{x}_{\mathrm{1}} =\mathrm{10}^{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}} }\\{\mathrm{x}_{\mathrm{2}} =\mathrm{10}^{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}} }\end{cases} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${x}_{\mathrm{1}} \centerdot{x}_{\mathrm{2}} =? \\ $$
