Question Number 144408 by mathdanisur last updated on 25/Jun/21

$$\boldsymbol{{lg}}\left(\mathrm{2}\right)=\boldsymbol{{x}} \\ $$$$\boldsymbol{{lg}}\left(\mathrm{7}\right)=\boldsymbol{{y}} \\ $$$$\boldsymbol{{lg}}_{\mathrm{5}} \left(\mathrm{9},\mathrm{8}\right)=? \\ $$
Answered by liberty last updated on 25/Jun/21
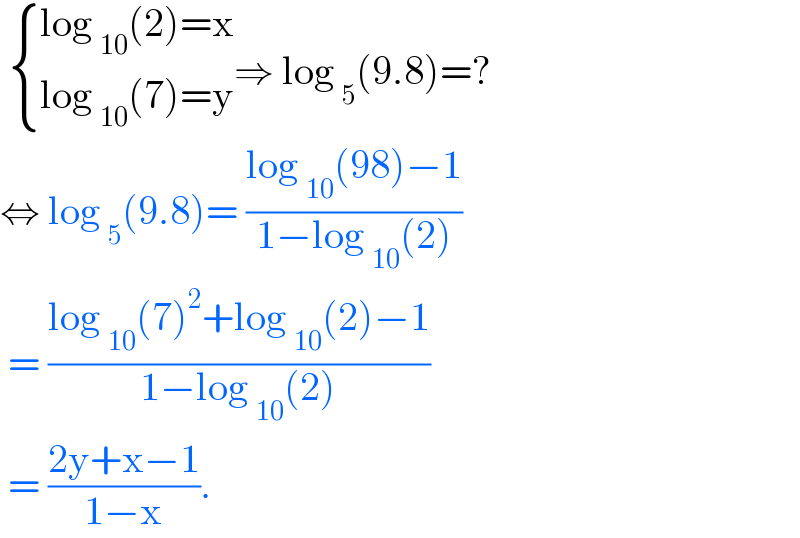
$$\:\begin{cases}{\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{2}\right)=\mathrm{x}}\\{\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{7}\right)=\mathrm{y}}\end{cases}\Rightarrow\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{9}.\mathrm{8}\right)=? \\ $$$$\Leftrightarrow\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{9}.\mathrm{8}\right)=\:\frac{\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{98}\right)−\mathrm{1}}{\mathrm{1}−\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{2}\right)} \\ $$$$\:=\:\frac{\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{7}\right)^{\mathrm{2}} +\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{1}−\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{2}\right)} \\ $$$$\:=\:\frac{\mathrm{2y}+\mathrm{x}−\mathrm{1}}{\mathrm{1}−\mathrm{x}}. \\ $$
Commented by mathdanisur last updated on 25/Jun/21

$${cool}\:{thanks}\:{Sir} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jun/21
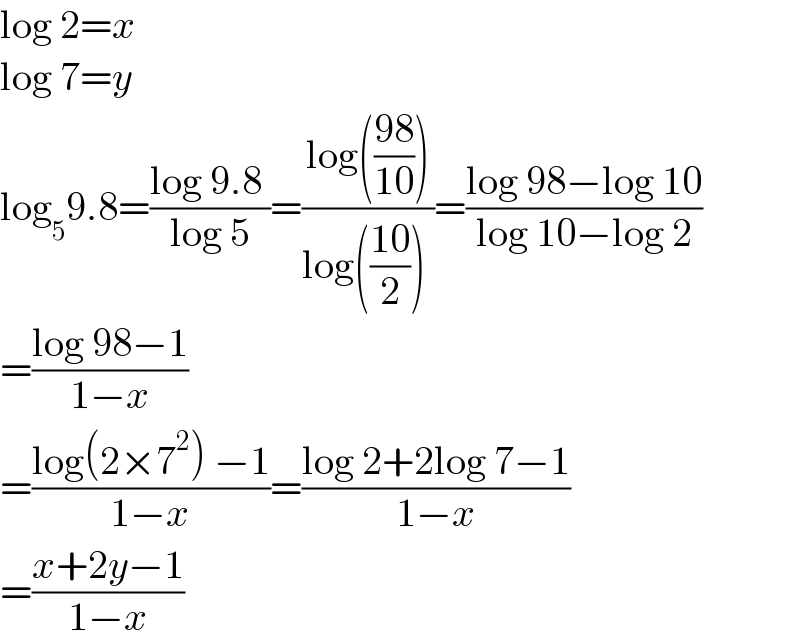
$$\mathrm{log}\:\mathrm{2}={x}\: \\ $$$$\mathrm{log}\:\mathrm{7}={y} \\ $$$$\mathrm{log}_{\mathrm{5}} \mathrm{9}.\mathrm{8}=\frac{\mathrm{log}\:\mathrm{9}.\mathrm{8}\:}{\mathrm{log}\:\mathrm{5}}=\frac{\mathrm{log}\left(\frac{\mathrm{98}}{\mathrm{10}}\right)}{\mathrm{log}\left(\frac{\mathrm{10}}{\mathrm{2}}\right)\:}=\frac{\mathrm{log}\:\mathrm{98}−\mathrm{log}\:\mathrm{10}}{\mathrm{log}\:\mathrm{10}−\mathrm{log}\:\mathrm{2}} \\ $$$$=\frac{\mathrm{log}\:\mathrm{98}−\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\frac{\mathrm{log}\left(\mathrm{2}×\mathrm{7}^{\mathrm{2}} \right)\:−\mathrm{1}}{\mathrm{1}−{x}}=\frac{\mathrm{log}\:\mathrm{2}+\mathrm{2log}\:\mathrm{7}−\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\frac{{x}+\mathrm{2}{y}−\mathrm{1}}{\mathrm{1}−{x}} \\ $$
Commented by mathdanisur last updated on 25/Jun/21
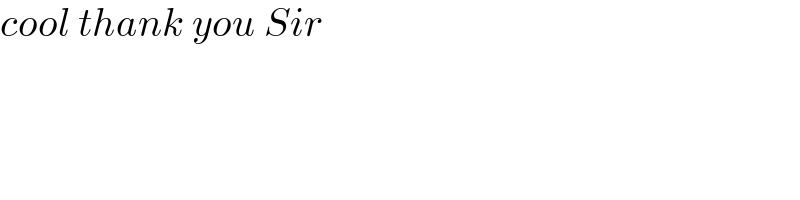
$${cool}\:{thank}\:{you}\:{Sir} \\ $$
Answered by justtry last updated on 25/Jun/21
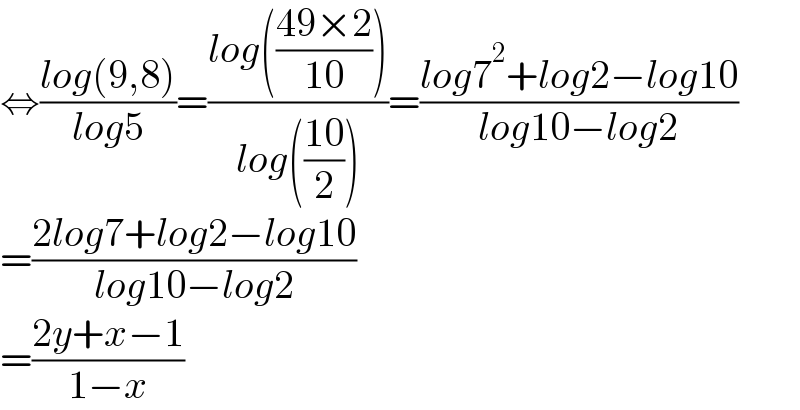
$$\Leftrightarrow\frac{{log}\left(\mathrm{9},\mathrm{8}\right)}{{log}\mathrm{5}}=\frac{{log}\left(\frac{\mathrm{49}×\mathrm{2}}{\mathrm{10}}\right)}{{log}\left(\frac{\mathrm{10}}{\mathrm{2}}\right)}=\frac{{log}\mathrm{7}^{\mathrm{2}} +{log}\mathrm{2}−{log}\mathrm{10}}{{log}\mathrm{10}−{log}\mathrm{2}} \\ $$$$=\frac{\mathrm{2}{log}\mathrm{7}+{log}\mathrm{2}−{log}\mathrm{10}}{{log}\mathrm{10}−{log}\mathrm{2}} \\ $$$$=\frac{\mathrm{2}{y}+{x}−\mathrm{1}}{\mathrm{1}−{x}} \\ $$
Commented by mathdanisur last updated on 25/Jun/21

$${Cool}\:{thanks}\:{Sir} \\ $$
