Question Number 90306 by Tony Lin last updated on 22/Apr/20
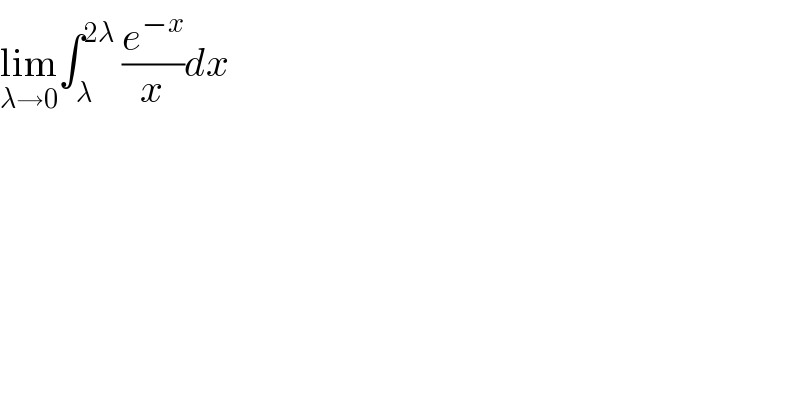
$$\underset{\lambda\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{\lambda} ^{\mathrm{2}\lambda} \:\frac{{e}^{−{x}} }{{x}}{dx} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
![∃ c∈]λ,2λ[ / ∫_λ ^(2λ) (e^(−x) /x)dx =e^(−c) ∫_λ ^(2λ) (dx/x) =e^(−c) ln∣((2λ)/λ)∣=e^(−c) ln(2) λ→0 ⇒c→0 ⇒lim_(λ→0) ∫_λ ^(2λ) (e^(−x) /x)dx =ln(2)](https://www.tinkutara.com/question/Q90349.png)
$$\left.\exists\:{c}\in\right]\lambda,\mathrm{2}\lambda\left[\:/\:\:\:\int_{\lambda} ^{\mathrm{2}\lambda} \:\frac{{e}^{−{x}} }{{x}}{dx}\:={e}^{−{c}} \:\int_{\lambda} ^{\mathrm{2}\lambda} \:\frac{{dx}}{{x}}\:={e}^{−{c}} {ln}\mid\frac{\mathrm{2}\lambda}{\lambda}\mid={e}^{−{c}} {ln}\left(\mathrm{2}\right)\right. \\ $$$$\lambda\rightarrow\mathrm{0}\:\Rightarrow{c}\rightarrow\mathrm{0}\:\Rightarrow{lim}_{\lambda\rightarrow\mathrm{0}} \:\:\:\int_{\lambda} ^{\mathrm{2}\lambda} \:\frac{{e}^{−{x}} }{{x}}{dx}\:={ln}\left(\mathrm{2}\right) \\ $$
Commented by Tony Lin last updated on 23/Apr/20

$${thanks}\:{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
![∫_λ ^(2λ) (e^(−x) /x)dx=∫_λ ^(2λ) (1/x)(1−x+(x^2 /(2!))−(x^3 /(3!))+(x^4 /(4!))+..)dx =∫_κ ^(2λ) ((1/x)−1+(x/(2!))−(x^2 /(3!))+(x^3 /(4!))+..)dx =∣lnx−x+(x^2 /(2×2!))−(x^3 /(3×3!))+..∣_λ ^(2λ) =ln2−∣x−(x^2 /(2×2!))+(x^3 /(3×3!))−..∣_λ ^(2λ) =ln2−[(λ)−((3λ^2 )/(2×2!))+((7λ^3 )/(3×3!))−..] so when λ→0 answer is ln2](https://www.tinkutara.com/question/Q90315.png)
$$\int_{\lambda} ^{\mathrm{2}\lambda} \frac{{e}^{−{x}} }{{x}}{dx}=\int_{\lambda} ^{\mathrm{2}\lambda} \frac{\mathrm{1}}{{x}}\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+..\right){dx} \\ $$$$=\int_{\kappa} ^{\mathrm{2}\lambda} \left(\frac{\mathrm{1}}{{x}}−\mathrm{1}+\frac{{x}}{\mathrm{2}!}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+..\right){dx} \\ $$$$=\mid{lnx}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}+..\mid_{\lambda} ^{\mathrm{2}\lambda} \\ $$$$={ln}\mathrm{2}−\mid{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}−..\mid_{\lambda} ^{\mathrm{2}\lambda} \\ $$$$={ln}\mathrm{2}−\left[\left(\lambda\right)−\frac{\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}!}+\frac{\mathrm{7}\lambda^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}−..\right] \\ $$$${so}\:{when}\:\lambda\rightarrow\mathrm{0} \\ $$$${answer}\:{is}\:{ln}\mathrm{2} \\ $$
Commented by peter frank last updated on 22/Apr/20

$${thank}\:{you} \\ $$
Commented by Tony Lin last updated on 23/Apr/20

$${thanks}\:{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 23/Apr/20

$${most}\:{welcome}\:{sir} \\ $$
Answered by maths mind last updated on 22/Apr/20

$$\frac{{e}^{−{x}} }{{x}}=\frac{\mathrm{1}+{e}^{−{x}} −\mathrm{1}}{{x}} \\ $$$$\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{\mathrm{1}+{e}^{−{x}} −\mathrm{1}}{{x}}{dx}=\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{\mathrm{1}}{{x}}{dx}+\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{{e}^{−{x}} −\mathrm{1}}{{x}}{dx} \\ $$$$\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{{e}^{−{x}} −\mathrm{1}}{{x}}{dx}=\mathrm{0} \\ $$$${e}^{−{x}} −\mathrm{1}=−{x}.{e}^{−{c}} \:\:{mean}\:{value} \\ $$$$\Rightarrow\mid\frac{{e}^{−{x}} −\mathrm{1}}{{x}}\mid\leqslant{e}^{−{a}} \\ $$$$\Rightarrow\mid\int_{{a}} ^{\mathrm{2}{a}} \frac{{e}^{−{x}} −\mathrm{1}}{{x}}{dx}\mid\leqslant\int_{{a}} ^{\mathrm{2}{a}} \mid\frac{{e}^{−{x}} −\mathrm{1}}{{x}}\mid{dx}\leqslant\int_{{a}} ^{\mathrm{2}{a}} {e}^{−{a}} {dx}={ae}^{−{a}} \rightarrow\mathrm{0} \\ $$$$\Rightarrow\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{{e}^{−{x}} −\mathrm{1}}{{x}}{dx}=\mathrm{0}\Rightarrow \\ $$$$\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{2}{a}} \frac{{e}^{−{x}} }{{x}}{dx}={ln}\left(\mathrm{2}\right) \\ $$
Commented by peter frank last updated on 22/Apr/20

$${help}\:{QN}\:\:\mathrm{90240} \\ $$
Commented by Tony Lin last updated on 23/Apr/20

$${thanks}\:{sir} \\ $$
