Question Number 121813 by bemath last updated on 12/Nov/20
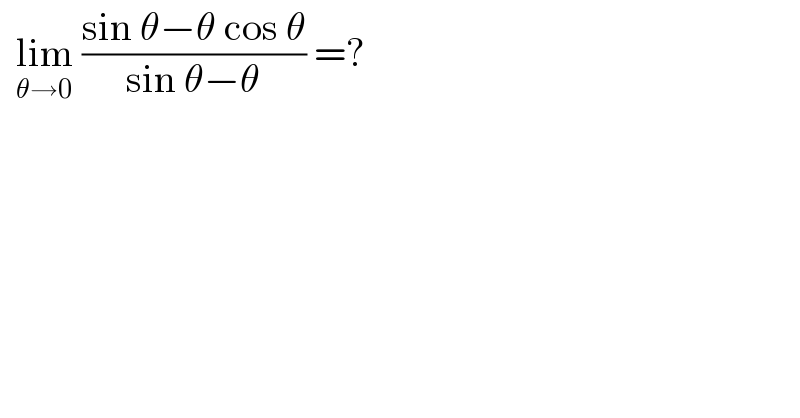
$$\:\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\theta−\theta\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta−\theta}\:=? \\ $$
Answered by bobhans last updated on 12/Nov/20

$$\:\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\theta−\theta\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta−\theta}\:=\: \\ $$$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\theta−\frac{\theta^{\mathrm{3}} }{\mathrm{6}}−\theta\left(\mathrm{1}−\frac{\theta^{\mathrm{2}} }{\mathrm{2}}\right)}{\theta−\frac{\theta^{\mathrm{3}} }{\mathrm{6}}−\theta}\:= \\ $$$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{2}\theta^{\mathrm{3}} }{\mathrm{6}}\right)}{−\left(\frac{\theta^{\mathrm{3}} }{\mathrm{6}}\right)}\:=\:−\mathrm{2}. \\ $$
Answered by liberty last updated on 12/Nov/20

$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\theta−\left(\mathrm{cos}\:\theta−\theta\:\mathrm{sin}\:\theta\right)}{\mathrm{cos}\:\theta−\mathrm{1}}\:= \\ $$$$\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\theta\:\mathrm{sin}\:\theta}{−\mathrm{2sin}\:^{\mathrm{2}} \left(\theta/\mathrm{2}\right)}\:=\:\frac{\mathrm{1}}{−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}\:=\:−\mathrm{2}.\blacktriangle \\ $$
Answered by Dwaipayan Shikari last updated on 12/Nov/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{2}!}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}=−\mathrm{2} \\ $$
