Question Number 83405 by jagoll last updated on 02/Mar/20
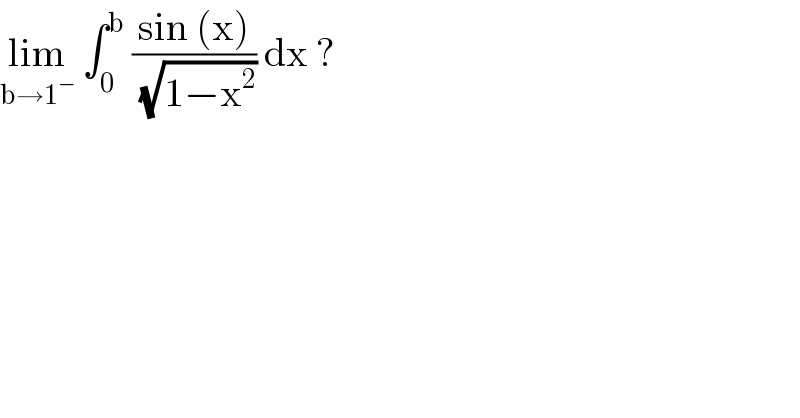
$$\underset{\mathrm{b}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\int_{\mathrm{0}} ^{\mathrm{b}} \:\frac{\mathrm{sin}\:\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:?\: \\ $$
Commented by mr W last updated on 02/Mar/20
![let x=sin θ =∫_0 ^(π/2) sin (sin θ) dθ =∫_0 ^(π/2) {2Σ_(k=0) ^∞ J_(2k+1) (1) sin (2k+1)θ}dθ =−2[Σ_(k=0) ^∞ ((J_(2k+1) (1))/(2k+1)) cos (2k+1)θ]_0 ^(π/2) =2Σ_(k=0) ^∞ ((J_(2k+1) (1))/(2k+1))](https://www.tinkutara.com/question/Q83410.png)
$${let}\:{x}=\mathrm{sin}\:\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}\:\left(\mathrm{sin}\:\theta\right)\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{J}_{\mathrm{2}{k}+\mathrm{1}} \left(\mathrm{1}\right)\:\mathrm{sin}\:\left(\mathrm{2}{k}+\mathrm{1}\right)\theta\right\}{d}\theta \\ $$$$=−\mathrm{2}\left[\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{J}_{\mathrm{2}{k}+\mathrm{1}} \left(\mathrm{1}\right)}{\mathrm{2}{k}+\mathrm{1}}\:\mathrm{cos}\:\left(\mathrm{2}{k}+\mathrm{1}\right)\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{J}_{\mathrm{2}{k}+\mathrm{1}} \left(\mathrm{1}\right)}{\mathrm{2}{k}+\mathrm{1}} \\ $$
Commented by jagoll last updated on 02/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
