Question Number 15773 by Mahmoud A.R last updated on 13/Jun/17
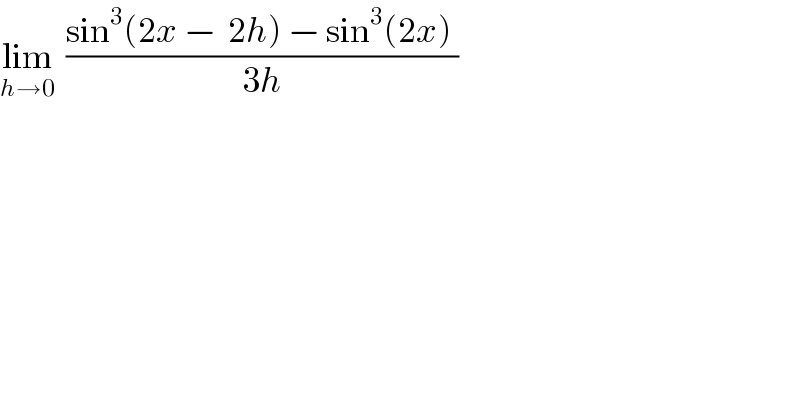
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2}{x}\:−\:\:\mathrm{2}{h}\right)\:−\:\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2}{x}\right)\:}{\mathrm{3}{h}} \\ $$
Answered by prakash jain last updated on 14/Jun/17
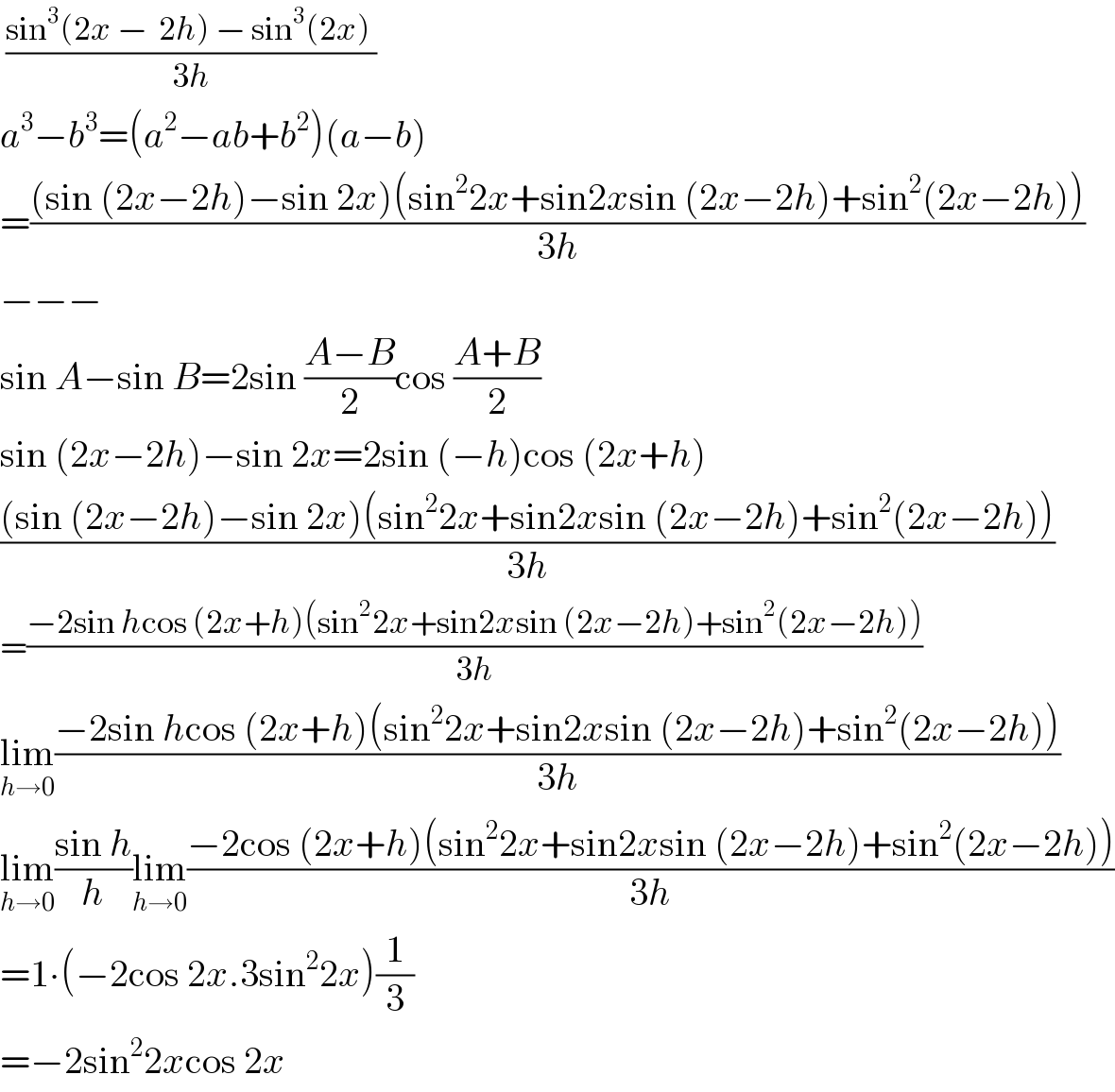
$$\:\frac{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2}{x}\:−\:\:\mathrm{2}{h}\right)\:−\:\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2}{x}\right)\:}{\mathrm{3}{h}} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)\left({a}−{b}\right) \\ $$$$=\frac{\left(\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)−\mathrm{sin}\:\mathrm{2}{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{sin2}{x}\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{2}{h}\right)\right)}{\mathrm{3}{h}} \\ $$$$−−− \\ $$$$\mathrm{sin}\:{A}−\mathrm{sin}\:{B}=\mathrm{2sin}\:\frac{{A}−{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}+{B}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)−\mathrm{sin}\:\mathrm{2}{x}=\mathrm{2sin}\:\left(−{h}\right)\mathrm{cos}\:\left(\mathrm{2}{x}+{h}\right) \\ $$$$\frac{\left(\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)−\mathrm{sin}\:\mathrm{2}{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{sin2}{x}\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{2}{h}\right)\right)}{\mathrm{3}{h}} \\ $$$$=\frac{−\mathrm{2sin}\:{h}\mathrm{cos}\:\left(\mathrm{2}{x}+{h}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{sin2}{x}\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{2}{h}\right)\right)}{\mathrm{3}{h}} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:{h}\mathrm{cos}\:\left(\mathrm{2}{x}+{h}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{sin2}{x}\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{2}{h}\right)\right)}{\mathrm{3}{h}} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{h}}{{h}}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2cos}\:\left(\mathrm{2}{x}+{h}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{sin2}{x}\mathrm{sin}\:\left(\mathrm{2}{x}−\mathrm{2}{h}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{2}{h}\right)\right)}{\mathrm{3}{h}} \\ $$$$=\mathrm{1}\centerdot\left(−\mathrm{2cos}\:\mathrm{2}{x}.\mathrm{3sin}^{\mathrm{2}} \mathrm{2}{x}\right)\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=−\mathrm{2sin}^{\mathrm{2}} \mathrm{2}{x}\mathrm{cos}\:\mathrm{2}{x} \\ $$
