Question Number 185329 by liuxinnan last updated on 20/Jan/23
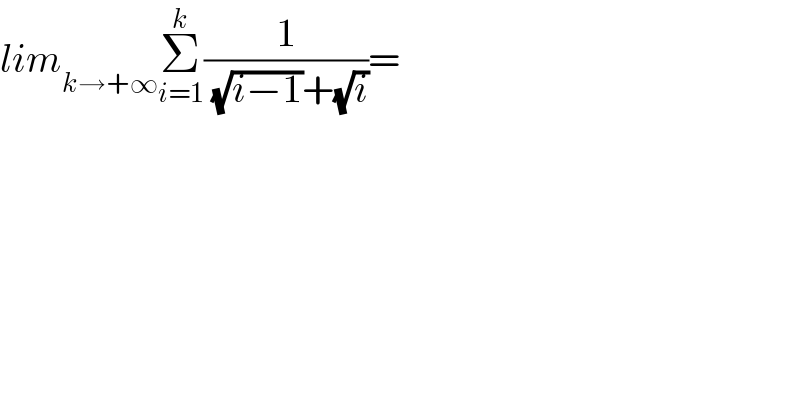
$${lim}_{{k}\rightarrow+\infty} \underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}= \\ $$
Answered by aleks041103 last updated on 20/Jan/23
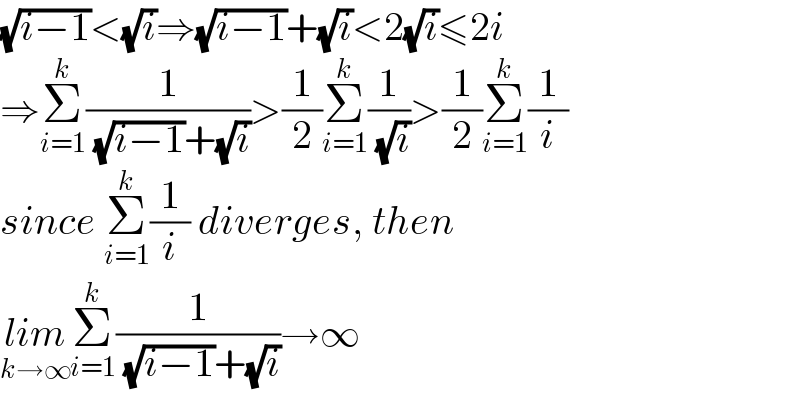
$$\sqrt{{i}−\mathrm{1}}<\sqrt{{i}}\Rightarrow\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}<\mathrm{2}\sqrt{{i}}\leqslant\mathrm{2}{i} \\ $$$$\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}>\frac{\mathrm{1}}{\mathrm{2}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}}}>\frac{\mathrm{1}}{\mathrm{2}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$${since}\:\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{i}}\:{diverges},\:{then} \\ $$$$\underset{{k}\rightarrow\infty} {{lim}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}\rightarrow\infty \\ $$
Answered by mr W last updated on 20/Jan/23
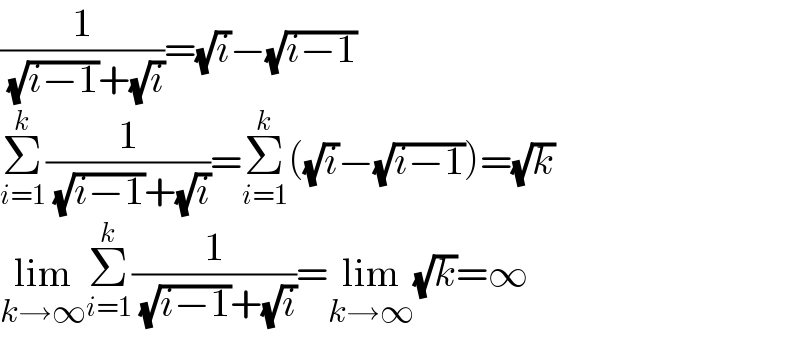
$$\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}=\sqrt{{i}}−\sqrt{{i}−\mathrm{1}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}=\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\sqrt{{i}}−\sqrt{{i}−\mathrm{1}}\right)=\sqrt{{k}} \\ $$$$\underset{{k}\rightarrow\infty} {\mathrm{lim}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}=\underset{{k}\rightarrow\infty} {\mathrm{lim}}\sqrt{{k}}=\infty \\ $$
