Question Number 186853 by liuxinnan last updated on 11/Feb/23
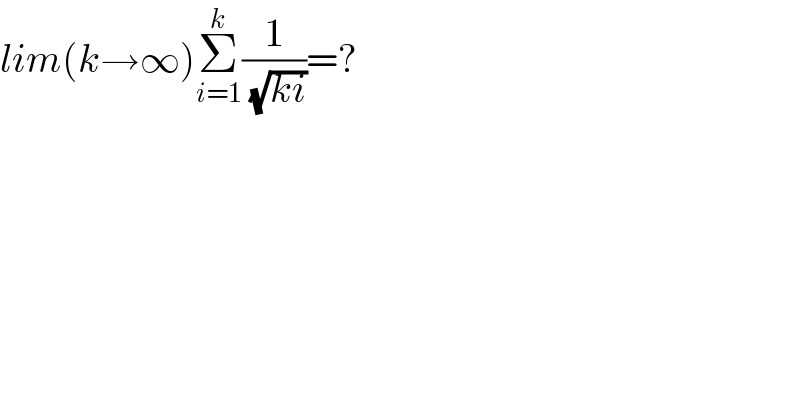
$${lim}\left({k}\rightarrow\infty\right)\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{ki}}}=? \\ $$
Answered by Ar Brandon last updated on 11/Feb/23
![L=lim_(k→∞) Σ_(i=1) ^k (1/( (√(ki))))=lim_(k→∞) (1/k)Σ_(i=1) ^k (√(k/i)) =∫_0 ^1 (1/( (√x)))dx=2[(√x)]_0 ^1 =2](https://www.tinkutara.com/question/Q186855.png)
$$\mathscr{L}=\underset{{k}\rightarrow\infty} {\mathrm{lim}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{ki}}}=\underset{{k}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{k}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\sqrt{\frac{{k}}{{i}}} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}}}{dx}=\mathrm{2}\left[\sqrt{{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2} \\ $$
