Question Number 162336 by mnjuly1970 last updated on 28/Dec/21
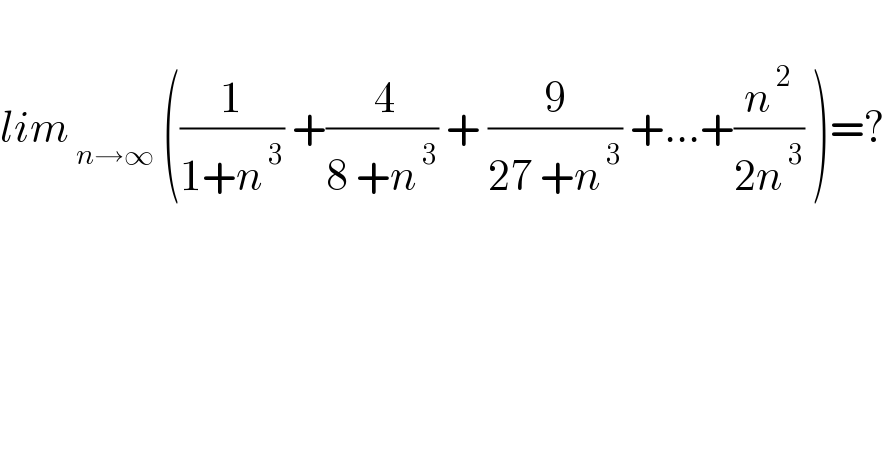
$$ \\ $$$${lim}_{\:{n}\rightarrow\infty} \:\left(\frac{\mathrm{1}}{\mathrm{1}+{n}^{\:\mathrm{3}} }\:+\frac{\:\mathrm{4}}{\mathrm{8}\:+{n}^{\:\mathrm{3}} }\:+\:\frac{\mathrm{9}}{\mathrm{27}\:+{n}^{\:\mathrm{3}} }\:+…+\frac{{n}^{\:\mathrm{2}} }{\mathrm{2}{n}^{\:\mathrm{3}} }\:\right)=? \\ $$$$ \\ $$
Answered by mindispower last updated on 28/Dec/21
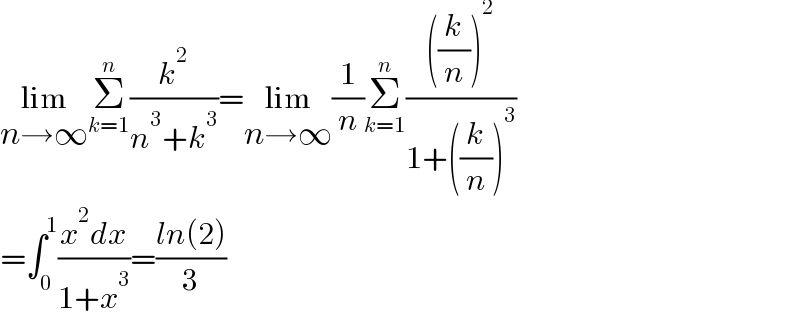
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{3}} +{k}^{\mathrm{3}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{3}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} {dx}}{\mathrm{1}+{x}^{\mathrm{3}} }=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 29/Dec/21
$$\:\:\:{grateful}\:{sir}\:{power} \\ $$
Commented by mindispower last updated on 29/Dec/21
$${pleasur}\:{sir}\:{have}\:{a}\:{great}\:{Day} \\ $$
