Question Number 99793 by bachamohamed last updated on 23/Jun/20
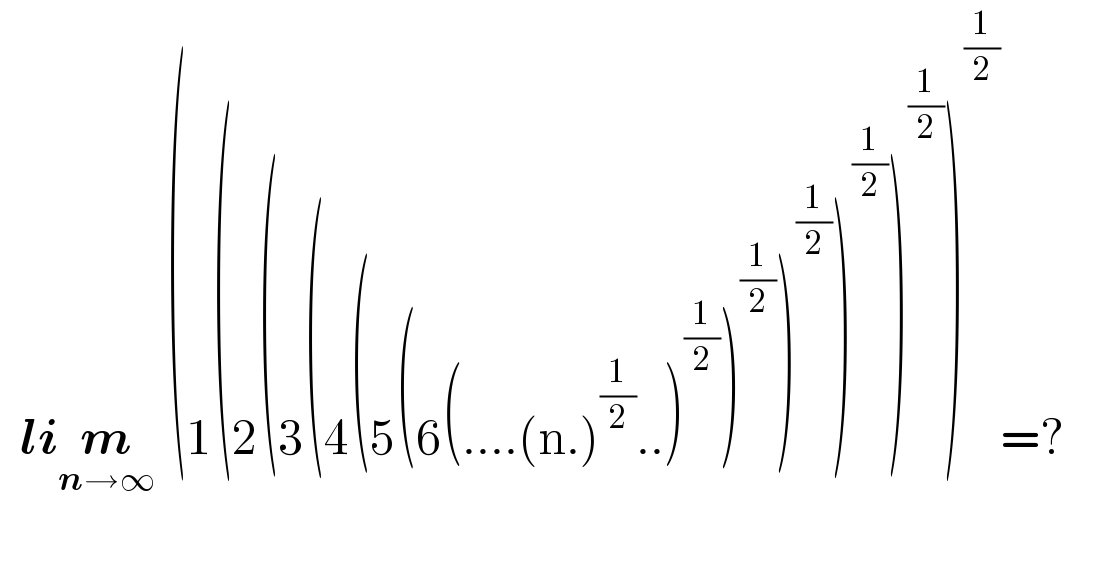
$$\:\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}}}\:\left(\mathrm{1}\left(\mathrm{2}\left(\mathrm{3}\left(\mathrm{4}\left(\mathrm{5}\left(\mathrm{6}\left(….\left(\mathrm{n}.\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ..\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =?\:\:\:\right. \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20

$$\sqrt{\mathrm{1}\sqrt{\mathrm{6}}} \\ $$$$ \\ $$
Commented by bachamohamed last updated on 23/Jun/20
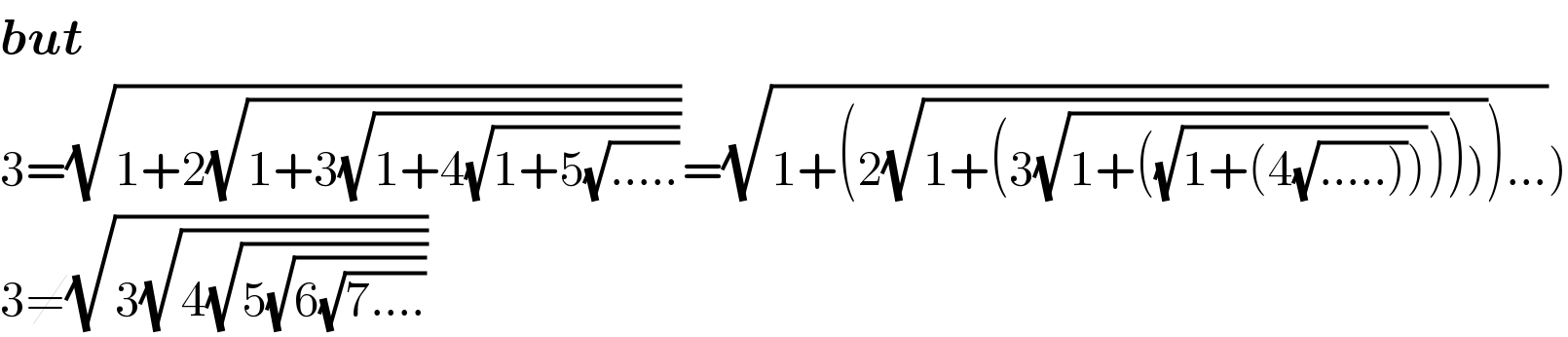
$$\boldsymbol{{but}}\: \\ $$$$\left.\mathrm{3}=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{…..}}}}}=\sqrt{\mathrm{1}+\left(\mathrm{2}\sqrt{\left.\mathrm{1}+\left(\mathrm{3}\sqrt{\mathrm{1}+\left(\sqrt{\mathrm{1}+\left(\mathrm{4}\sqrt{\left……\right)}\right)}\right)}\right)\right)}\right)…}\right) \\ $$$$\mathrm{3}\neq\sqrt{\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}….}}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20

$${I}\:{have}\:{come}\:{to}\:{know}\:{that}\:{my}\:{process}\:{is}\:{wrong}.\:{I}\:{am}\:{trying}\:{another}\:{method} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20
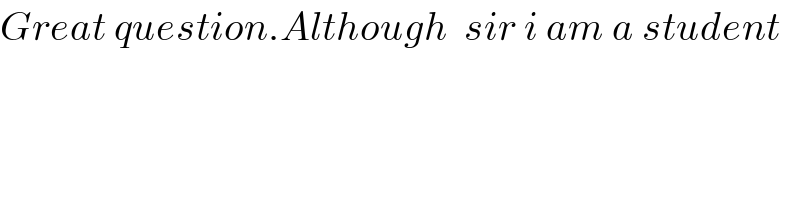
$${Great}\:{question}.{Although}\:\:{sir}\:{i}\:{am}\:{a}\:{student} \\ $$
