Question Number 161133 by qaz last updated on 12/Dec/21
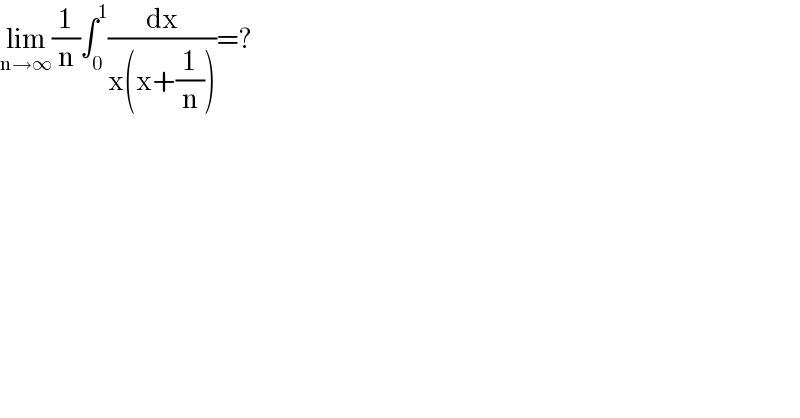
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{n}}\right)}=? \\ $$
Answered by ArielVyny last updated on 12/Dec/21
![(1/n)∫_0 ^1 (dx/(x(x+(1/n))))=∫_0 ^1 (1/x)−(1/((x+(1/n))))dx =[ln(x)−ln(x+(1/n))]_0 ^1 =[ln(x/(x+(1/n)))]_0 ^1 =0 lim_(n→∞) = (1/n)∫_0 ^1 (dx/(x(x+(1/n))))=0](https://www.tinkutara.com/question/Q161137.png)
$$\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}\left({x}+\frac{\mathrm{1}}{{n}}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{{n}}\right)}{dx} \\ $$$$=\left[{ln}\left({x}\right)−{ln}\left({x}+\frac{\mathrm{1}}{{n}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\left[{ln}\frac{{x}}{{x}+\frac{\mathrm{1}}{{n}}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{0} \\ $$$${lim}_{{n}\rightarrow\infty} =\:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}\left({x}+\frac{\mathrm{1}}{{n}}\right)}=\mathrm{0} \\ $$$$ \\ $$
Commented by mr W last updated on 12/Dec/21
![how [ln(x/(x+(1/n)))]_0 ^1 =0 ?](https://www.tinkutara.com/question/Q161144.png)
$${how}\:\left[{ln}\frac{{x}}{{x}+\frac{\mathrm{1}}{{n}}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{0}\:? \\ $$
