Question Number 122458 by benjo_mathlover last updated on 17/Nov/20

$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{n}}\:}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}}+\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}+…+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{n}−\mathrm{1}}+\sqrt{\mathrm{2}{n}+\mathrm{1}}}\:\right)=? \\ $$
Answered by liberty last updated on 17/Nov/20
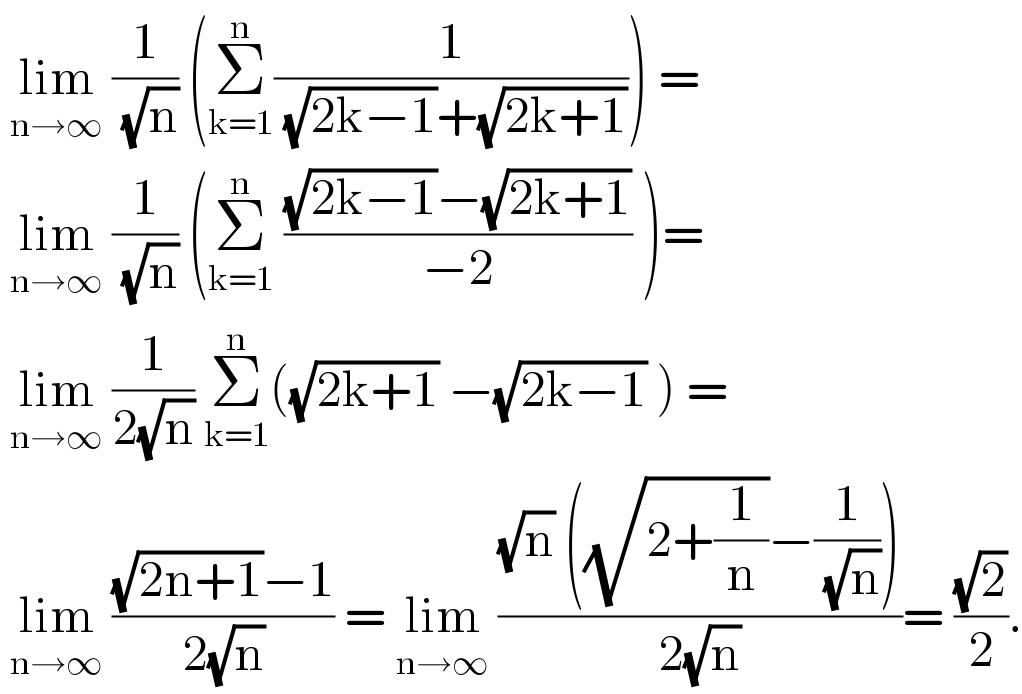
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2k}−\mathrm{1}}+\sqrt{\mathrm{2k}+\mathrm{1}}}\right)\:= \\ $$$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\frac{\sqrt{\mathrm{2k}−\mathrm{1}}−\sqrt{\mathrm{2k}+\mathrm{1}}}{−\mathrm{2}}\:\right)= \\ $$$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{n}}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\sqrt{\mathrm{2k}+\mathrm{1}}\:−\sqrt{\mathrm{2k}−\mathrm{1}}\:\right)\:= \\ $$$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2n}+\mathrm{1}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{n}}}\:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{n}}\:\left(\sqrt{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\right)}{\mathrm{2}\sqrt{\mathrm{n}}}=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}. \\ $$
Answered by Dwaipayan Shikari last updated on 17/Nov/20

$$\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{{n}}}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{1}}+\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}+….+\sqrt{\mathrm{2}{n}+\mathrm{1}}−\sqrt{\mathrm{2}{n}−\mathrm{1}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\left(\sqrt{\mathrm{2}{n}+\mathrm{1}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{2}+\frac{\mathrm{1}}{{n}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$
