Question Number 95849 by bobhans last updated on 28/May/20
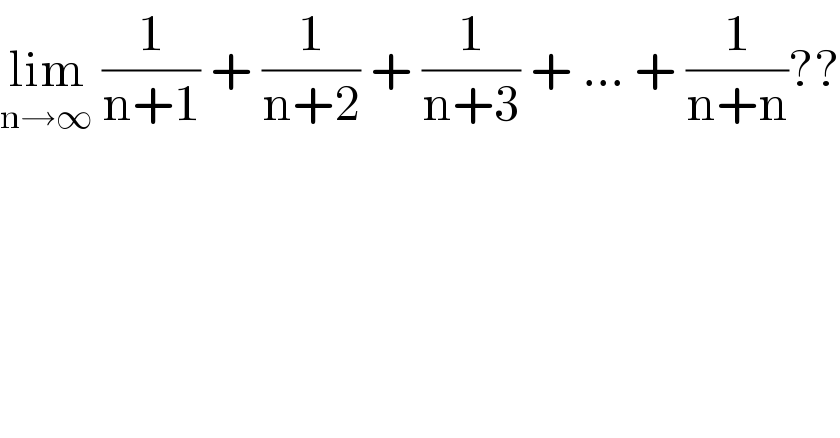
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}\:+\:…\:+\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{n}}?? \\ $$
Answered by john santu last updated on 28/May/20
![lim_(n→∞) Σ_(k = 1) ^n ((1/(n+k))) = lim_(n→∞) Σ_(k = 1) ^n (1/n)((1/(1+(k/n)))) = ∫_1 ^2 (dx/x) = [ ln (x) ] _1^2 = ln (2).](https://www.tinkutara.com/question/Q95850.png)
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\right)\:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}}\right)\: \\ $$$$=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{{dx}}{{x}}\:=\:\:\left[\:\mathrm{ln}\:\left(\mathrm{x}\right)\:\right]\:_{\mathrm{1}} ^{\mathrm{2}} \:=\:\mathrm{ln}\:\left(\mathrm{2}\right). \\ $$
Answered by mathmax by abdo last updated on 28/May/20
![let U_n =(1/(n+1)) +(1/(n+2)) +(1/(n+3))+....+(1/(n+n)) ⇒U_n =Σ_(k=1) ^n (1/(n+k)) =(1/n)Σ_(k=1) ^n (1/(1+(k/n))) ⇒U_n is a Rieman sum ⇒lim_(n→+∞) U_n =∫_0 ^1 (dx/(1+x)) =[ln(1+x)]_0 ^1 =ln(2)](https://www.tinkutara.com/question/Q95926.png)
$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}+….+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{n}}\:\Rightarrow\mathrm{U}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}}\:\Rightarrow\mathrm{U}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{Rieman}\:\mathrm{sum}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}} \\ $$$$=\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{ln}\left(\mathrm{2}\right) \\ $$
