lim-n-1-n-1-2-3-3-n-n-

Question Number 174951 by infinityaction last updated on 14/Aug/22

$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\left[\mathrm{1}+\sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{3}}+…^{{n}} \sqrt{{n}}\right] \\ $$

Answered by TheHoneyCat last updated on 16/Aug/22

There′s a theorem that sates that U_n →_(n→∞) l ∈ R^_ ⇒ lim_(n→∞) Σ_(k=0) ^n U_k =l Now ^n (√n)=n^(1/n) =exp(((ln n)/n)) since ln n /n→0 ^n (√n)→exp(0)=1 Thus: your limit is 1.

$$\mathrm{There}'\mathrm{s}\:\mathrm{a}\:\mathrm{theorem}\:\mathrm{that}\:\mathrm{sates}\:\mathrm{that} \\ $$$${U}_{{n}} \:\:\underset{{n}\rightarrow\infty} {\rightarrow}{l}\:\in\:\overset{\_} {\mathbb{R}}\:\Rightarrow\:\mathrm{lim}_{{n}\rightarrow\infty} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{U}_{{k}} ={l} \\ $$$$ \\ $$$$\mathrm{Now} \\ $$$$\:^{{n}} \sqrt{{n}}={n}^{\mathrm{1}/{n}} =\mathrm{exp}\left(\frac{\mathrm{ln}\:{n}}{{n}}\right)\: \\ $$$$\mathrm{since}\:\mathrm{ln}\:{n}\:/{n}\rightarrow\mathrm{0} \\ $$$$\:^{{n}} \sqrt{{n}}\rightarrow\mathrm{exp}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Thus}:\: \\ $$$$\mathrm{your}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{1}. \\ $$

Commented by TheHoneyCat last updated on 16/Aug/22

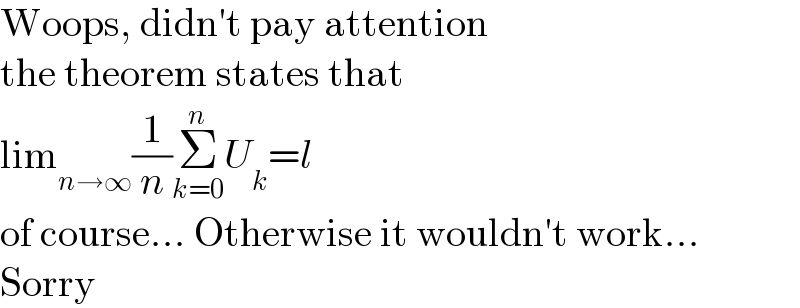
Woops, didn′t pay attention the theorem states that lim_(n→∞) (1/n)Σ_(k=0) ^n U_k =l of course... Otherwise it wouldn′t work... Sorry

$$\mathrm{Woops},\:\mathrm{didn}'\mathrm{t}\:\mathrm{pay}\:\mathrm{attention} \\ $$$$\mathrm{the}\:\mathrm{theorem}\:\mathrm{states}\:\mathrm{that}\: \\ $$$$\mathrm{lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{U}_{{k}} ={l} \\ $$$$\mathrm{of}\:\mathrm{course}…\:\mathrm{Otherwise}\:\mathrm{it}\:\mathrm{wouldn}'\mathrm{t}\:\mathrm{work}… \\ $$$$\mathrm{Sorry} \\ $$

Facebook Tweet Pin

lim-n-1-n-1-2-3-3-n-n-

Leave a Reply Cancel reply