Question Number 95325 by ~blr237~ last updated on 24/May/20
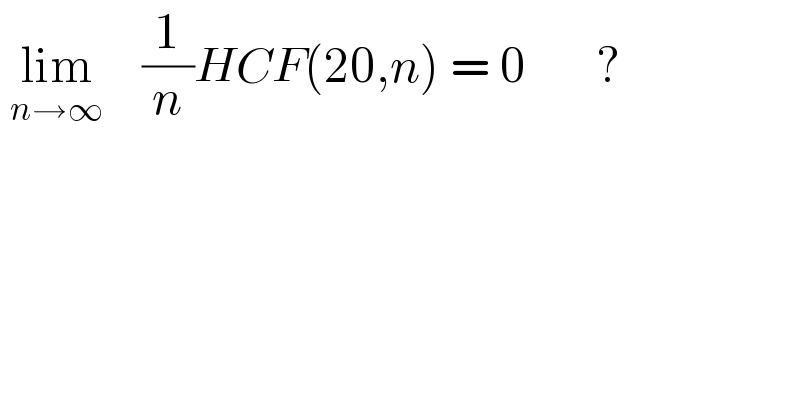
$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{1}}{{n}}{HCF}\left(\mathrm{20},{n}\right)\:=\:\mathrm{0}\:\:\:\:\:\:\:? \\ $$
Commented by mr W last updated on 24/May/20
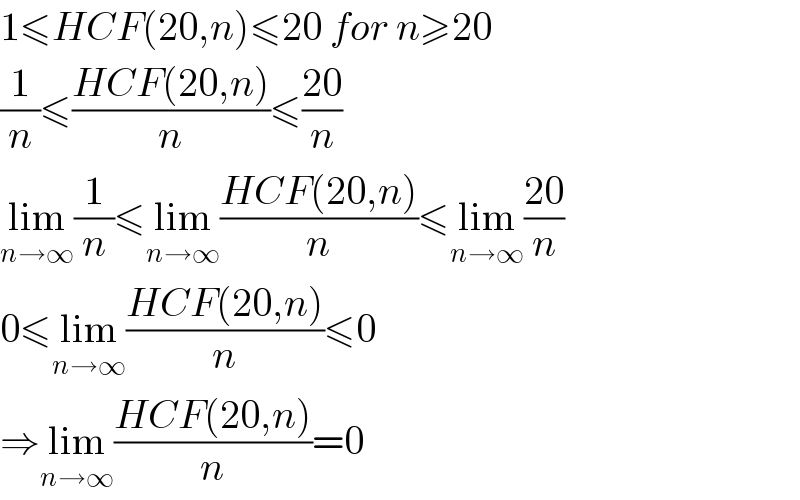
$$\mathrm{1}\leqslant{HCF}\left(\mathrm{20},{n}\right)\leqslant\mathrm{20}\:{for}\:{n}\geqslant\mathrm{20} \\ $$$$\frac{\mathrm{1}}{{n}}\leqslant\frac{{HCF}\left(\mathrm{20},{n}\right)}{{n}}\leqslant\frac{\mathrm{20}}{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{HCF}\left(\mathrm{20},{n}\right)}{{n}}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{20}}{{n}} \\ $$$$\mathrm{0}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{HCF}\left(\mathrm{20},{n}\right)}{{n}}\leqslant\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{HCF}\left(\mathrm{20},{n}\right)}{{n}}=\mathrm{0} \\ $$
