Question Number 88065 by arcana last updated on 08/Apr/20
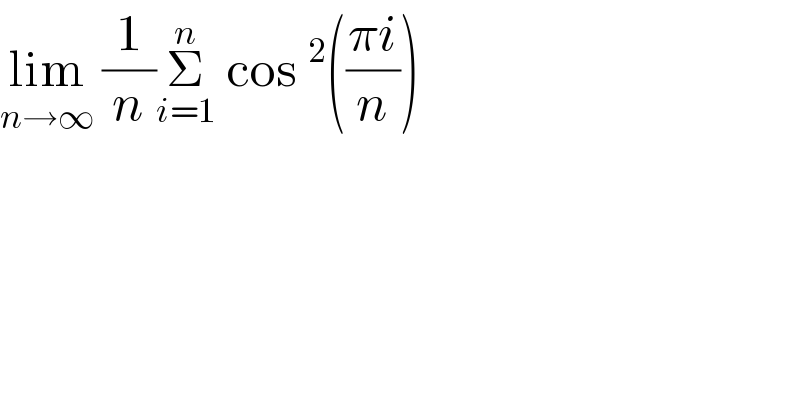
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi{i}}{{n}}\right) \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
![∫_a ^b f(x)dx =lim_(n→+∞) ((b−a)/n)Σ_(k=1) ^n f(a+((k(b−a))/n)) (Rieman sum) ⇒ lim_(n→∞) (1/n)Σ_(i=1) ^n cos^2 (((iπ)/n)) =(1/π)lim_(n→+∞) ((π−0)/n)Σ_(i=1) ^n cos^2 (((i(π−0))/n)) =(1/π)∫_0 ^π cos^2 x dx =(1/(2π))∫_0 ^π (1+cos(2x))dx =(1/2) +(1/(4π))[sin(2x)]_0 ^π =(1/2)](https://www.tinkutara.com/question/Q88156.png)
$$\int_{{a}} ^{{b}} \:{f}\left({x}\right){dx}\:={lim}_{{n}\rightarrow+\infty} \frac{{b}−{a}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} \:{f}\left({a}+\frac{{k}\left({b}−{a}\right)}{{n}}\right)\:\:\left({Rieman}\:{sum}\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} \:\frac{\mathrm{1}}{{n}}\sum_{{i}=\mathrm{1}} ^{{n}} \:{cos}^{\mathrm{2}} \left(\frac{{i}\pi}{{n}}\right)\:=\frac{\mathrm{1}}{\pi}{lim}_{{n}\rightarrow+\infty} \:\frac{\pi−\mathrm{0}}{{n}}\sum_{{i}=\mathrm{1}} ^{{n}} {cos}^{\mathrm{2}} \left(\frac{{i}\left(\pi−\mathrm{0}\right)}{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} \:{cos}^{\mathrm{2}} {x}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}\pi}\left[{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by arcana last updated on 08/Apr/20

$${gracias} \\ $$
Commented by abdomathmax last updated on 10/Apr/20

$${you}\:{are}\:{welcome} \\ $$
