lim-n-1-n-k-1-n-1-k-3-n-3-1-2-

Question Number 104890 by Ar Brandon last updated on 24/Jul/20

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\mathrm{1}+\frac{\mathrm{k}^{\mathrm{3}} }{\mathrm{n}^{\mathrm{3}} }\right]^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Answered by abdomathmax last updated on 24/Jul/20

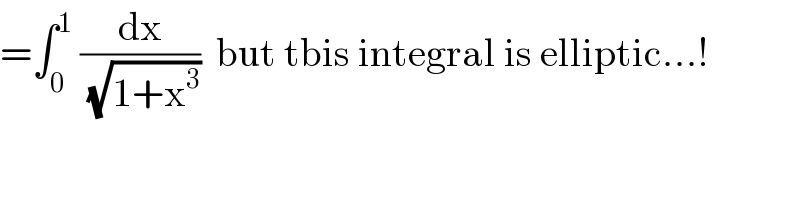
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}\:\:\mathrm{but}\:\mathrm{tbis}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{elliptic}…! \\ $$

Commented by Ar Brandon last updated on 24/Jul/20

So, no solution, Sir ? ��

Commented by mathmax by abdo last updated on 24/Jul/20

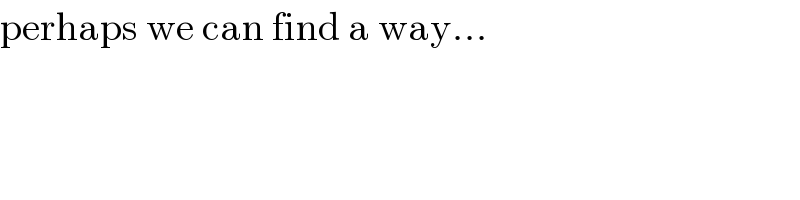
$$\mathrm{perhaps}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{a}\:\mathrm{way}… \\ $$

Commented by Ar Brandon last updated on 24/Jul/20

Alright, cool

Terms of Service
Privacy Policy
Contact: info@tinkutara.com