Question Number 96602 by Ar Brandon last updated on 03/Jun/20
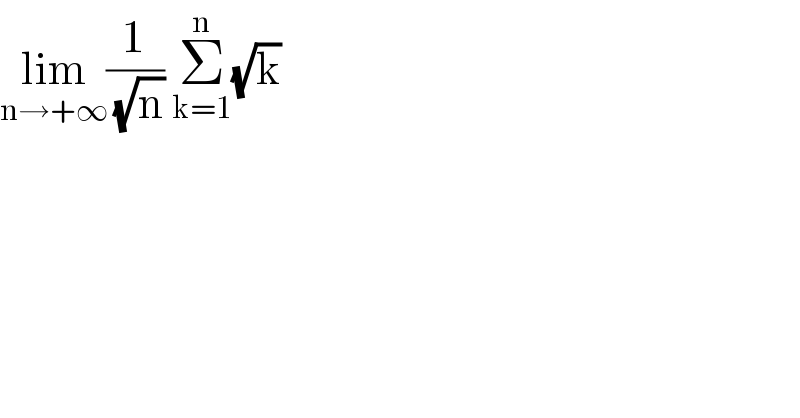
$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{k}} \\ $$
Answered by Sourav mridha last updated on 03/Jun/20
![by inspection Σ_(k=1) ^n (√(k )) this is a diverging series as n⇒∞. proof: using Eular−Maclaurin integration formula.... Σ_(k=1) ^n (√k) =[((16n^2 +12n−5(√n) +1)/(24(√n)))] approximate result..but okkk.. now,lim_(n→∞) (1/( (√n)))Σ_(k=1) ^n (√k) =lim_(n→∞) [((16n+12−(5/( (√n)))+(1/n))/(24))] =∞..](https://www.tinkutara.com/question/Q96611.png)
$$\boldsymbol{{by}}\:\boldsymbol{{inspection}}\:\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\sqrt{\boldsymbol{{k}}\:}\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{a}} \\ $$$$\boldsymbol{{diverging}}\:\boldsymbol{{series}}\:\boldsymbol{{as}}\:\boldsymbol{{n}}\Rightarrow\infty. \\ $$$$\: \\ $$$$\boldsymbol{{proof}}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{using}}\:\boldsymbol{{E}}\mathrm{ular}−\boldsymbol{{Maclaurin}} \\ $$$$\boldsymbol{{integration}}\:\boldsymbol{{formula}}…. \\ $$$$\:\:\:\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\sqrt{\boldsymbol{{k}}}\:=\left[\frac{\mathrm{16}\boldsymbol{{n}}^{\mathrm{2}} +\mathrm{12}\boldsymbol{{n}}−\mathrm{5}\sqrt{\boldsymbol{{n}}}\:+\mathrm{1}}{\mathrm{24}\sqrt{\boldsymbol{{n}}}}\right] \\ $$$$\boldsymbol{{approximate}}\:\boldsymbol{{result}}..\boldsymbol{{but}}\:\boldsymbol{{okkk}}.. \\ $$$$\boldsymbol{{now}},\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{n}}}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\sqrt{\boldsymbol{{k}}}\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{16}\boldsymbol{{n}}+\mathrm{12}−\frac{\mathrm{5}}{\:\sqrt{\boldsymbol{{n}}}}+\frac{\mathrm{1}}{\boldsymbol{{n}}}}{\mathrm{24}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\infty.. \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
![S_n =(1/( (√n)))Σ_(k=1) ^n (√k) ⇒S_n =Σ_(k=1) ^n (√(k/n))=n×(1/n)Σ_(k=1) ^n (√(k/n)) but lim_(n→+∞) (1/n)(√(k/n))=∫_0 ^1 (√x)dx =∫_0 ^1 x^(1/2) dx =[(2/3)x^(3/2) ]_0 ^1 =(2/3) ⇒ lim_(n→+∞) S_n =lim_(n→+∞) ((2n)/3) =+∞](https://www.tinkutara.com/question/Q96633.png)
$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\sqrt{\mathrm{k}}\:\Rightarrow\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\frac{\mathrm{k}}{\mathrm{n}}}=\mathrm{n}×\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\frac{\mathrm{k}}{\mathrm{n}}} \\ $$$$\mathrm{but}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}}\sqrt{\frac{\mathrm{k}}{\mathrm{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dx}\:=\left[\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{2n}}{\mathrm{3}}\:=+\infty \\ $$
Answered by maths mind last updated on 03/Jun/20
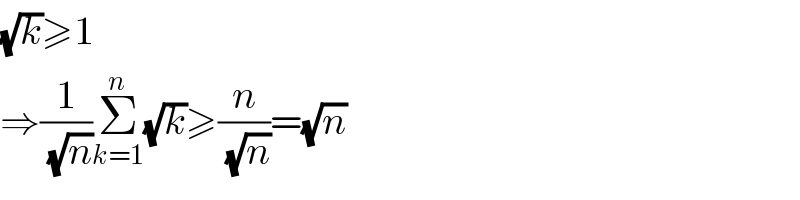
$$\sqrt{{k}}\geqslant\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{{k}}\geqslant\frac{{n}}{\:\sqrt{{n}}}=\sqrt{{n}} \\ $$
