Question Number 98788 by Ar Brandon last updated on 16/Jun/20
![lim_(n→∞) (1/n)[ (n+1)(n+2)...(n+n)_ ^ ]^(1/n)](https://www.tinkutara.com/question/Q98788.png)
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\left[\:\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)…\left(\mathrm{n}+\mathrm{n}\right)_{} ^{} \right]^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$
Answered by Ar Brandon last updated on 16/Jun/20
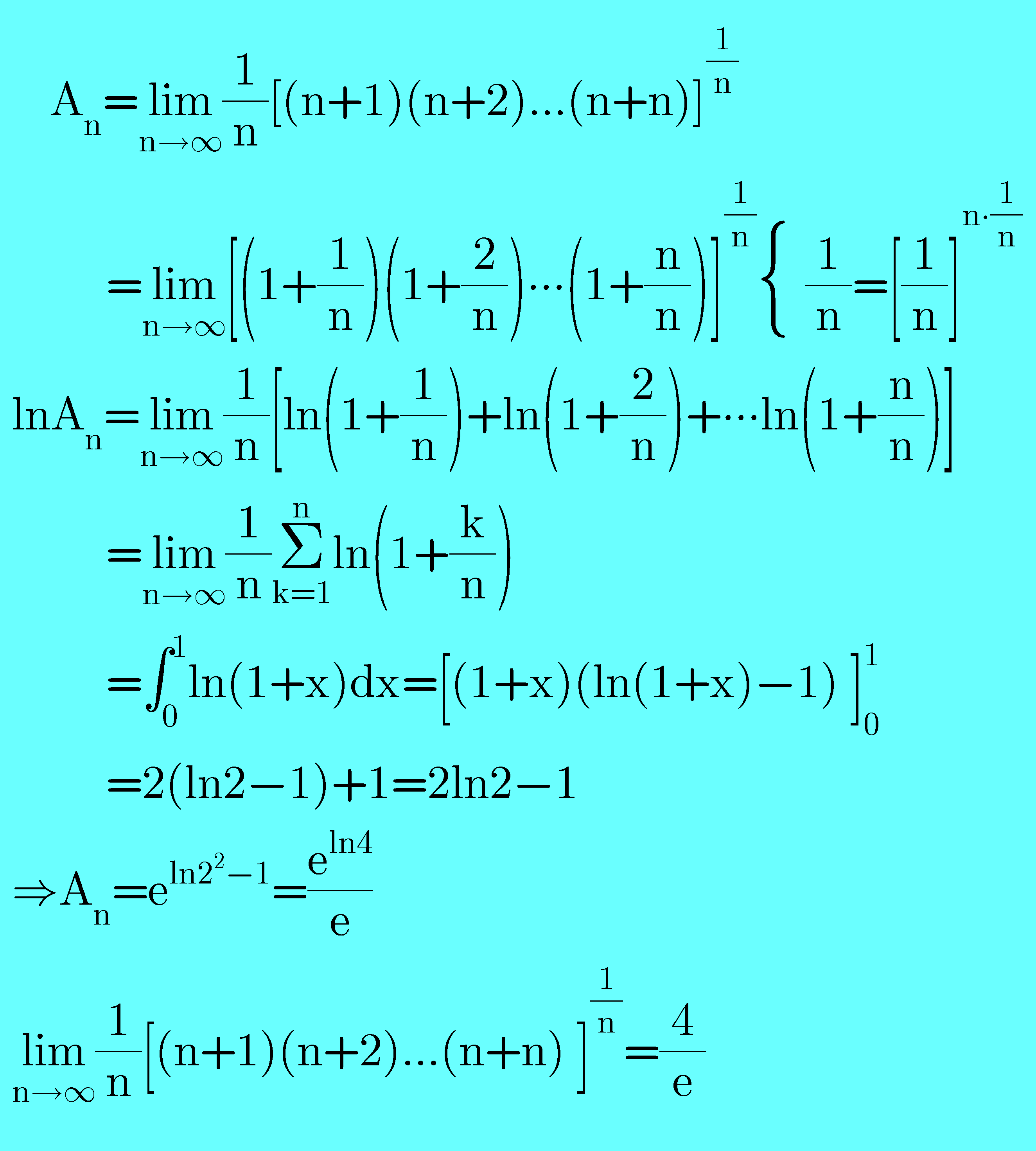
Answered by mathmax by abdo last updated on 16/Jun/20
![A_n =(1/n)(Π_(k=1) ^n (n+k))^(1/n) ⇒ln(A_n ) =−ln(n) +(1/n)ln(Π_(k=1) ^n (n+k)) =−ln(n) +(1/n)Σ_(k=1) ^n ln(n+k) =−ln(n) +(1/n) Σ_(k=1) ^n (ln(n) +ln(1+(k/n))) =(1/n) Σ_(k=1) ^n ln(1+(k/n))→∫_0 ^1 ln(1+x)dx and ∫_0 ^1 ln(1+x)dx =[xln(1+x)]_0 ^1 −∫_0 ^1 (x/(1+x))dx =ln(2)−∫_0 ^1 ((x+1−1)/(1+x))dx =ln(2)−1 +ln(2) =2ln(2)−1 ⇒ lim_(n→+∞) A_n =e^(2ln(2)−1) =(4/e)](https://www.tinkutara.com/question/Q98840.png)
$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\mathrm{n}+\mathrm{k}\right)\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\mathrm{ln}\left(\mathrm{A}_{\mathrm{n}} \right)\:=−\mathrm{ln}\left(\mathrm{n}\right)\:+\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{n}+\mathrm{k}\right)\right) \\ $$$$=−\mathrm{ln}\left(\mathrm{n}\right)\:+\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right) \\ $$$$=−\mathrm{ln}\left(\mathrm{n}\right)\:+\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{ln}\left(\mathrm{n}\right)\:+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)\:=\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx}\:=\left[\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}+\mathrm{1}−\mathrm{1}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{1}\:+\mathrm{ln}\left(\mathrm{2}\right)\:=\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1}} \:=\frac{\mathrm{4}}{\mathrm{e}} \\ $$
