Question Number 128626 by john_santu last updated on 09/Jan/21
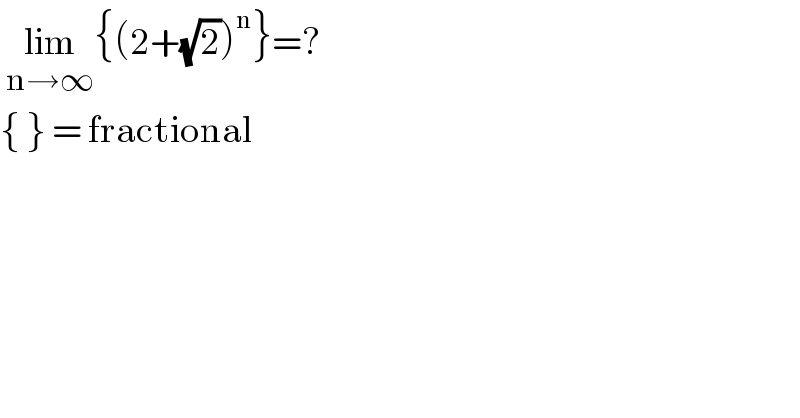
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \right\}=? \\ $$$$\left\{\:\right\}\:=\:\mathrm{fractional}\: \\ $$$$ \\ $$
Commented by liberty last updated on 09/Jan/21

$$\left\{{x}\right\}\:=\:{x}−\lfloor{x}\rfloor\: \\ $$
Answered by mnjuly1970 last updated on 09/Jan/21
![solution: t_n :=(2+(√2) )^n +(2−(√2) )^n ∈^(why?) N because: t_n =Σ_(k=0) ^n { ((n),(k) ) (2)^(n−k) ((√2) )^k (1+(−1)^k ) =Σ_(k=_(k ∈ N_( E) ) 0) ^n { ((n),(k) ) 2^(n−k+(k/2)+1) } =Σ_(k=_(k∈N_( E) ) 0) { ((n),(k) ) 2^([n+(k/2)+1∈ N]) }∈N b ut we know: 0<( 2−(√2) )^n <1 ∴ 0< 1−(2−(√(2 )) )^n <1 lim_(n→∞ ) (1−(2−(√2) )^n )=1 {(2+(√2) )^n }={t_n −(2−(√2) )^n } ={t_n −1+1−(2−(√2) )^n } ∴lim_(n→∞) {(2+(√2) )^n }=1 note:{t_n −1}=0](https://www.tinkutara.com/question/Q128658.png)
$${solution}: \\ $$$$\:{t}_{{n}} :=\left(\mathrm{2}+\sqrt{\mathrm{2}}\:\right)^{{n}} +\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{{n}} \overset{{why}?} {\in}\mathbb{N}\: \\ $$$${because}:\:{t}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\left(\mathrm{2}\right)^{{n}−{k}} \left(\sqrt{\mathrm{2}}\:\right)^{{k}} \left(\mathrm{1}+\left(−\mathrm{1}\right)^{{k}} \right)\right. \\ $$$$=\underset{{k}\underset{{k}\:\in\:\mathbb{N}_{\:{E}} } {=}\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\mathrm{2}^{{n}−{k}+\frac{{k}}{\mathrm{2}}+\mathrm{1}} \right\} \\ $$$$=\underset{{k}\underset{{k}\in\mathbb{N}_{\:{E}} } {=}\mathrm{0}} {\sum}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\mathrm{2}^{\left[{n}+\frac{{k}}{\mathrm{2}}+\mathrm{1}\in\:\mathbb{N}\right]} \right\}\in\mathbb{N} \\ $$$$\:\:{b}\:{ut}\:{we}\:{know}:\:\mathrm{0}<\left(\:\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{{n}} <\mathrm{1} \\ $$$$\:\therefore\:\mathrm{0}<\:\mathrm{1}−\left(\mathrm{2}−\sqrt{\mathrm{2}\:}\:\right)^{{n}} \:<\mathrm{1} \\ $$$$\:\:\:\:\:{lim}_{{n}\rightarrow\infty\:} \left(\mathrm{1}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{{n}} \right)=\mathrm{1} \\ $$$$\:\:\left\{\left(\mathrm{2}+\sqrt{\mathrm{2}}\:\right)^{{n}} \right\}=\left\{{t}_{{n}} −\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{{n}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left\{{t}_{{n}} −\mathrm{1}+\mathrm{1}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{{n}} \right\}\:\: \\ $$$$\:\:\therefore{lim}_{{n}\rightarrow\infty} \left\{\left(\mathrm{2}+\sqrt{\mathrm{2}}\:\right)^{{n}} \right\}=\mathrm{1} \\ $$$$\:\:\:\:\:\:{note}:\left\{{t}_{{n}} −\mathrm{1}\right\}=\mathrm{0} \\ $$
