Question Number 103749 by bobhans last updated on 17/Jul/20
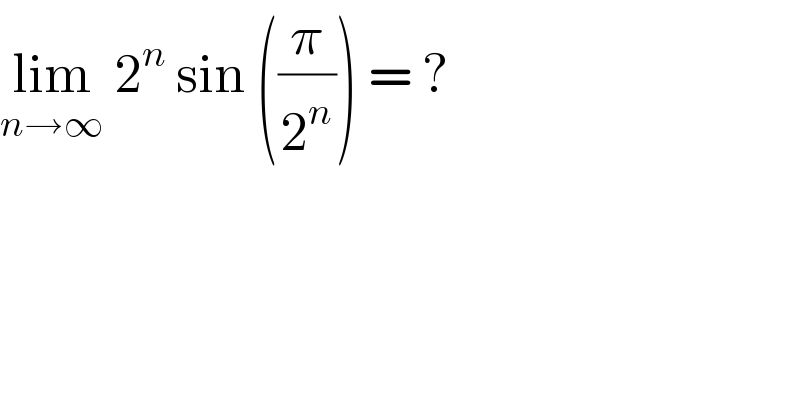
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{2}^{{n}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)\:=\:? \\ $$
Answered by bramlex last updated on 17/Jul/20
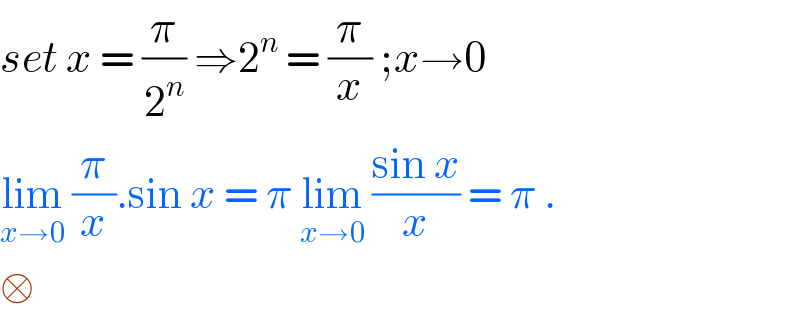
$${set}\:{x}\:=\:\frac{\pi}{\mathrm{2}^{{n}} }\:\Rightarrow\mathrm{2}^{{n}} \:=\:\frac{\pi}{{x}}\:;{x}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\pi}{{x}}.\mathrm{sin}\:{x}\:=\:\pi\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{{x}}\:=\:\pi\:. \\ $$$$\square \\ $$
Answered by Sobir last updated on 17/Jul/20

$${the}\:\:{ansver}\:{is}\:\:\:\pi \\ $$
Answered by Dwaipayan Shikari last updated on 17/Jul/20

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\pi\frac{{sin}\frac{\pi}{\mathrm{2}^{{n}} }}{\frac{\pi}{\mathrm{2}^{{n}} }}=\pi \\ $$
