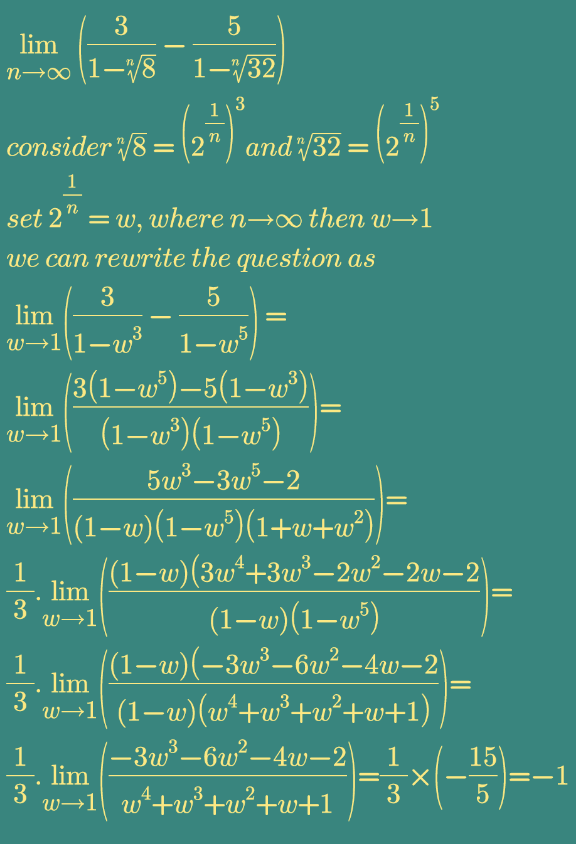Question Number 109763 by Karani last updated on 25/Aug/20
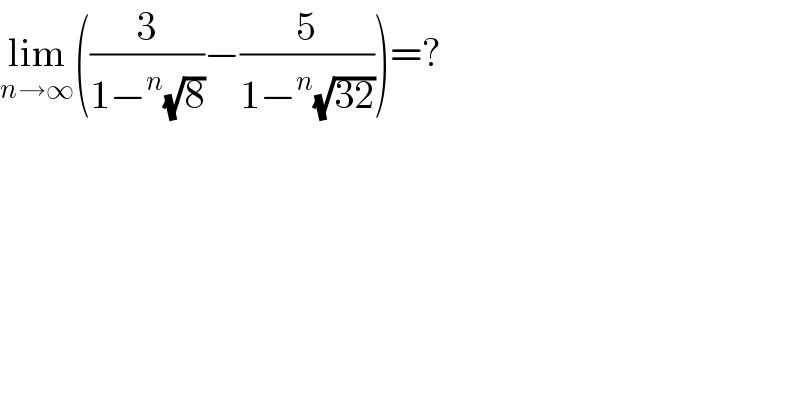
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}}{\mathrm{1}−^{{n}} \sqrt{\mathrm{8}}}−\frac{\mathrm{5}}{\mathrm{1}−^{{n}} \sqrt{\mathrm{32}}}\right)=? \\ $$
Answered by bemath last updated on 25/Aug/20
![▽((♭e)/(math))Δ lim_(n→∞) ((3−3 ((32))^(1/(n )) −5+5 (8)^(1/n) )/(1−((32))^(1/n) −(8)^(1/n) +((256))^(1/(n )) )) = let (1/n) = t { ((n→∞)),((t→0)) :} lim_(t→0) [((−2−3 (32)^t +5 (8)^t )/(1−(32)^t −(8)^t +(256)^t )) ]= lim_(t→0) [((−2−3(2^t )^5 +5(2^t )^3 )/(1−(2^t )^5 −(2^t )^3 +(2^t )^8 )) ]= set 2^t = m,m→1 lim_(m→1) [((5m^3 −3m^5 −2)/(m^8 −m^3 −m^5 +1))]= L′Hopital lim_(m→1) [((15m^2 −15m^4 )/(8m^7 −3m^2 −5m^4 )) ]= lim_(m→1) [((15−15m^2 )/(8m^5 −3−5m^2 )) ] = lim_(m→1) [((−30m)/(40m^4 −10m)) ] = ((−30)/(30))=−1](https://www.tinkutara.com/question/Q109780.png)
$$\:\:\:\bigtriangledown\frac{\flat{e}}{{math}}\Delta \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}\:\sqrt[{{n}\:}]{\mathrm{32}}−\mathrm{5}+\mathrm{5}\:\sqrt[{{n}}]{\mathrm{8}}}{\mathrm{1}−\sqrt[{{n}}]{\mathrm{32}}−\sqrt[{{n}}]{\mathrm{8}}\:+\sqrt[{{n}\:}]{\mathrm{256}}}\:= \\ $$$${let}\:\frac{\mathrm{1}}{{n}}\:=\:{t}\:\begin{cases}{{n}\rightarrow\infty}\\{{t}\rightarrow\mathrm{0}}\end{cases} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{−\mathrm{2}−\mathrm{3}\:\left(\mathrm{32}\right)^{{t}} +\mathrm{5}\:\left(\mathrm{8}\right)^{{t}} }{\mathrm{1}−\left(\mathrm{32}\right)^{{t}} −\left(\mathrm{8}\right)^{{t}} +\left(\mathrm{256}\right)^{{t}} }\:\right]= \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{−\mathrm{2}−\mathrm{3}\left(\mathrm{2}^{{t}} \right)^{\mathrm{5}} +\mathrm{5}\left(\mathrm{2}^{{t}} \right)^{\mathrm{3}} }{\mathrm{1}−\left(\mathrm{2}^{{t}} \right)^{\mathrm{5}} −\left(\mathrm{2}^{{t}} \right)^{\mathrm{3}} +\left(\mathrm{2}^{{t}} \right)^{\mathrm{8}} }\:\right]= \\ $$$${set}\:\mathrm{2}^{{t}} =\:{m},{m}\rightarrow\mathrm{1} \\ $$$$\underset{{m}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{5}{m}^{\mathrm{3}} −\mathrm{3}{m}^{\mathrm{5}} −\mathrm{2}}{{m}^{\mathrm{8}} −{m}^{\mathrm{3}} −{m}^{\mathrm{5}} +\mathrm{1}}\right]= \\ $$$${L}'{Hopital} \\ $$$$\underset{{m}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{15}{m}^{\mathrm{2}} −\mathrm{15}{m}^{\mathrm{4}} }{\mathrm{8}{m}^{\mathrm{7}} −\mathrm{3}{m}^{\mathrm{2}} −\mathrm{5}{m}^{\mathrm{4}} }\:\right]= \\ $$$$\underset{{m}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{15}−\mathrm{15}{m}^{\mathrm{2}} }{\mathrm{8}{m}^{\mathrm{5}} −\mathrm{3}−\mathrm{5}{m}^{\mathrm{2}} }\:\right]\:= \\ $$$$\underset{{m}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{−\mathrm{30}{m}}{\mathrm{40}{m}^{\mathrm{4}} −\mathrm{10}{m}}\:\right]\:=\:\frac{−\mathrm{30}}{\mathrm{30}}=−\mathrm{1} \\ $$
Answered by Her_Majesty last updated on 25/Aug/20
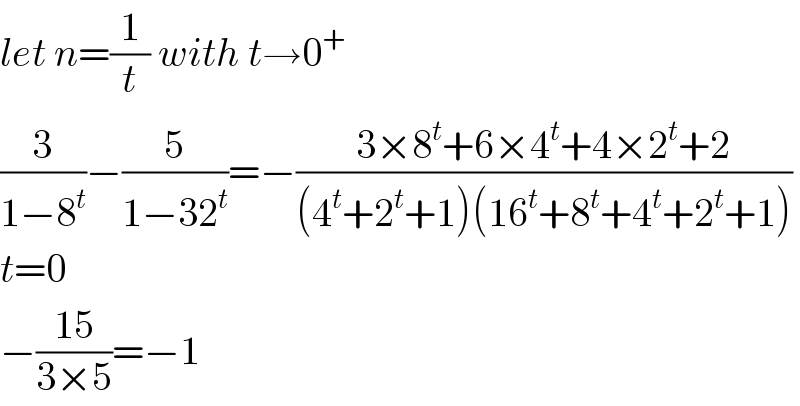
$${let}\:{n}=\frac{\mathrm{1}}{{t}}\:{with}\:{t}\rightarrow\mathrm{0}^{+} \\ $$$$\frac{\mathrm{3}}{\mathrm{1}−\mathrm{8}^{{t}} }−\frac{\mathrm{5}}{\mathrm{1}−\mathrm{32}^{{t}} }=−\frac{\mathrm{3}×\mathrm{8}^{{t}} +\mathrm{6}×\mathrm{4}^{{t}} +\mathrm{4}×\mathrm{2}^{{t}} +\mathrm{2}}{\left(\mathrm{4}^{{t}} +\mathrm{2}^{{t}} +\mathrm{1}\right)\left(\mathrm{16}^{{t}} +\mathrm{8}^{{t}} +\mathrm{4}^{{t}} +\mathrm{2}^{{t}} +\mathrm{1}\right)} \\ $$$${t}=\mathrm{0} \\ $$$$−\frac{\mathrm{15}}{\mathrm{3}×\mathrm{5}}=−\mathrm{1} \\ $$
Answered by john santu last updated on 25/Aug/20