lim-n-3-n-2-2-5-n-1-3-n-2-5-n-1-

Question Number 57866 by Mikael_Marshall last updated on 13/Apr/19

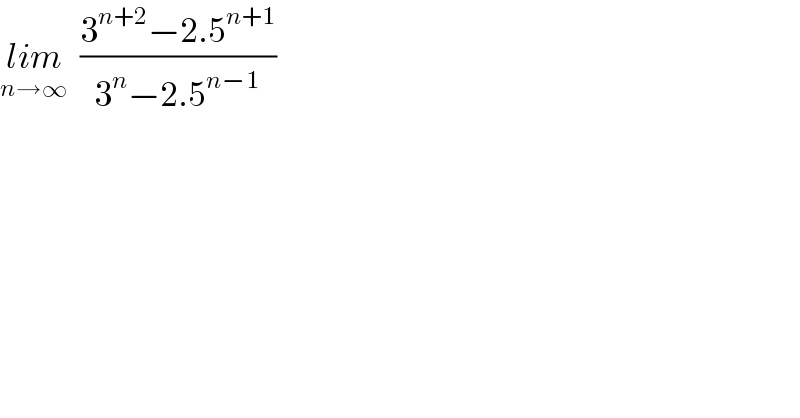
$$\underset{{n}\rightarrow\infty} {{lim}}\:\:\frac{\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}.\mathrm{5}^{{n}+\mathrm{1}} }{\mathrm{3}^{{n}} −\mathrm{2}.\mathrm{5}^{{n}−\mathrm{1}} } \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19

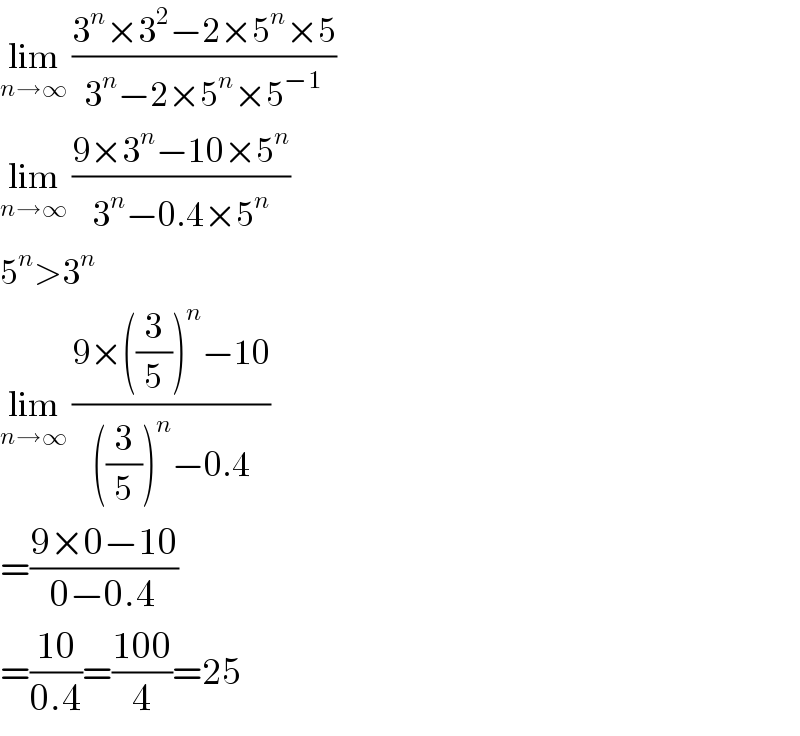
lim_(n→∞) ((3^n ×3^2 −2×5^n ×5)/(3^n −2×5^n ×5^(−1) )) lim_(n→∞) ((9×3^n −10×5^n )/(3^n −0.4×5^n )) 5^n >3^n lim_(n→∞) ((9×((3/5))^n −10)/(((3/5))^n −0.4)) =((9×0−10)/(0−0.4)) =((10)/(0.4))=((100)/4)=25

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}^{{n}} ×\mathrm{3}^{\mathrm{2}} −\mathrm{2}×\mathrm{5}^{{n}} ×\mathrm{5}}{\mathrm{3}^{{n}} −\mathrm{2}×\mathrm{5}^{{n}} ×\mathrm{5}^{−\mathrm{1}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{9}×\mathrm{3}^{{n}} −\mathrm{10}×\mathrm{5}^{{n}} }{\mathrm{3}^{{n}} −\mathrm{0}.\mathrm{4}×\mathrm{5}^{{n}} } \\ $$$$\mathrm{5}^{{n}} >\mathrm{3}^{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{9}×\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}} −\mathrm{10}}{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}} −\mathrm{0}.\mathrm{4}} \\ $$$$=\frac{\mathrm{9}×\mathrm{0}−\mathrm{10}}{\mathrm{0}−\mathrm{0}.\mathrm{4}} \\ $$$$=\frac{\mathrm{10}}{\mathrm{0}.\mathrm{4}}=\frac{\mathrm{100}}{\mathrm{4}}=\mathrm{25} \\ $$

Commented by Mikael_Marshall last updated on 13/Apr/19

$${yes}\:{Sir} \\ $$

Answered by Kunal12588 last updated on 13/Apr/19

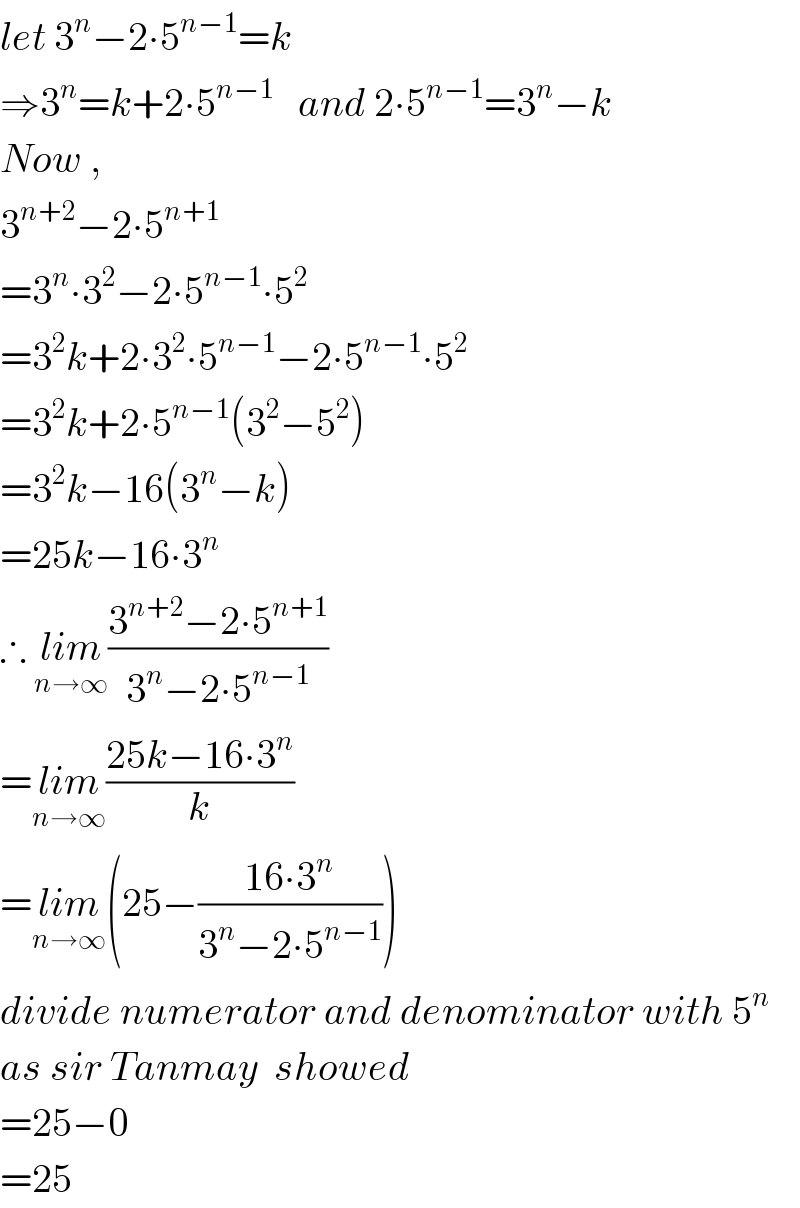
let 3^n −2∙5^(n−1) =k ⇒3^n =k+2∙5^(n−1) and 2∙5^(n−1) =3^n −k Now , 3^(n+2) −2∙5^(n+1) =3^n ∙3^2 −2∙5^(n−1) ∙5^2 =3^2 k+2∙3^2 ∙5^(n−1) −2∙5^(n−1) ∙5^2 =3^2 k+2∙5^(n−1) (3^2 −5^2 ) =3^2 k−16(3^n −k) =25k−16∙3^n ∴ lim_(n→∞) ((3^(n+2) −2∙5^(n+1) )/(3^n −2∙5^(n−1) )) =lim_(n→∞) ((25k−16∙3^n )/k) =lim_(n→∞) (25−((16∙3^n )/(3^n −2∙5^(n−1) ))) divide numerator and denominator with 5^n as sir Tanmay showed =25−0 =25

$${let}\:\mathrm{3}^{{n}} −\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} ={k} \\ $$$$\Rightarrow\mathrm{3}^{{n}} ={k}+\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} \:\:\:{and}\:\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} =\mathrm{3}^{{n}} −{k} \\ $$$${Now}\:, \\ $$$$\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}\centerdot\mathrm{5}^{{n}+\mathrm{1}} \\ $$$$=\mathrm{3}^{{n}} \centerdot\mathrm{3}^{\mathrm{2}} −\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} \centerdot\mathrm{5}^{\mathrm{2}} \\ $$$$=\mathrm{3}^{\mathrm{2}} {k}+\mathrm{2}\centerdot\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{5}^{{n}−\mathrm{1}} −\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} \centerdot\mathrm{5}^{\mathrm{2}} \\ $$$$=\mathrm{3}^{\mathrm{2}} {k}+\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} \left(\mathrm{3}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} \right) \\ $$$$=\mathrm{3}^{\mathrm{2}} {k}−\mathrm{16}\left(\mathrm{3}^{{n}} −{k}\right) \\ $$$$=\mathrm{25}{k}−\mathrm{16}\centerdot\mathrm{3}^{{n}} \\ $$$$\therefore\:\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}\centerdot\mathrm{5}^{{n}+\mathrm{1}} }{\mathrm{3}^{{n}} −\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} } \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{25}{k}−\mathrm{16}\centerdot\mathrm{3}^{{n}} }{{k}} \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left(\mathrm{25}−\frac{\mathrm{16}\centerdot\mathrm{3}^{{n}} }{\mathrm{3}^{{n}} −\mathrm{2}\centerdot\mathrm{5}^{{n}−\mathrm{1}} }\right)\:\:\:\:\: \\ $$$${divide}\:{numerator}\:{and}\:{denominator}\:{with}\:\mathrm{5}^{{n}} \\ $$$${as}\:{sir}\:{Tanmay}\:\:{showed} \\ $$$$=\mathrm{25}−\mathrm{0} \\ $$$$=\mathrm{25} \\ $$

Commented by Mikael_Marshall last updated on 13/Apr/19

$${thanks}\:{Sir} \\ $$

Facebook Tweet Pin

lim-n-3-n-2-2-5-n-1-3-n-2-5-n-1-

Leave a Reply Cancel reply