Question Number 166926 by mathlove last updated on 02/Mar/22

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}=? \\ $$
Answered by JDamian last updated on 02/Mar/22

$$\mathrm{0} \\ $$
Answered by Mathspace last updated on 02/Mar/22
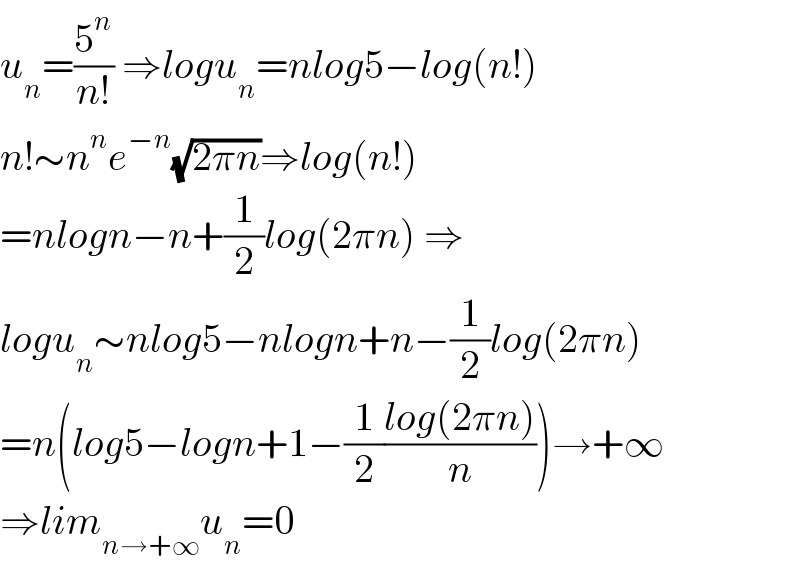
$${u}_{{n}} =\frac{\mathrm{5}^{{n}} }{{n}!}\:\Rightarrow{logu}_{{n}} ={nlog}\mathrm{5}−{log}\left({n}!\right) \\ $$$${n}!\sim{n}^{{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\Rightarrow{log}\left({n}!\right) \\ $$$$={nlogn}−{n}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi{n}\right)\:\Rightarrow \\ $$$${logu}_{{n}} \sim{nlog}\mathrm{5}−{nlogn}+{n}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi{n}\right) \\ $$$$={n}\left({log}\mathrm{5}−{logn}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\frac{{log}\left(\mathrm{2}\pi{n}\right)}{{n}}\right)\rightarrow+\infty \\ $$$$\Rightarrow{lim}_{{n}\rightarrow+\infty} {u}_{{n}} =\mathrm{0} \\ $$
Commented by mathlove last updated on 03/Mar/22

$${thanks} \\ $$
Answered by mr W last updated on 03/Mar/22

$$\frac{\mathrm{5}^{{n}} }{{n}!}>\frac{\mathrm{1}}{{n}!} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}>\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}!}=\mathrm{0} \\ $$$$ \\ $$$$\frac{\mathrm{5}^{{n}} }{{n}!}=\frac{\mathrm{5}^{\mathrm{12}} ×\mathrm{5}×..×\mathrm{5}}{\mathrm{12}!×\mathrm{13}×\mathrm{14}×…×{n}} \\ $$$$=\left(\frac{\mathrm{5}^{\mathrm{12}} }{\mathrm{12}!}\right)×\left(\frac{\mathrm{5}}{\mathrm{13}}\right)×\left(\frac{\mathrm{5}}{\mathrm{14}}\right)×…×\left(\frac{\mathrm{5}}{{n}}\right) \\ $$$$<\left(\frac{\mathrm{9}\:\mathrm{765}\:\mathrm{265}}{\mathrm{19}\:\mathrm{160}\:\mathrm{964}}\right)×\left(\frac{\mathrm{5}}{\mathrm{13}}\right)^{{n}−\mathrm{12}} \\ $$$$<\left(\frac{\mathrm{5}}{\mathrm{13}}\right)^{{n}−\mathrm{12}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{5}}{\mathrm{13}}\right)^{{n}−\mathrm{12}} =\mathrm{0} \\ $$$$\mathrm{0}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}\:<\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}\:=\mathrm{0} \\ $$
