Question Number 57850 by Mikael_Marshall last updated on 13/Apr/19
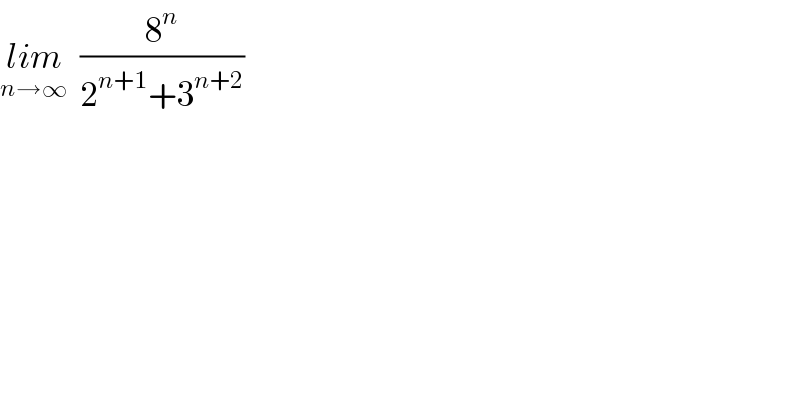
$$\underset{{n}\rightarrow\infty} {{lim}}\:\:\frac{\mathrm{8}^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{3}^{{n}+\mathrm{2}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
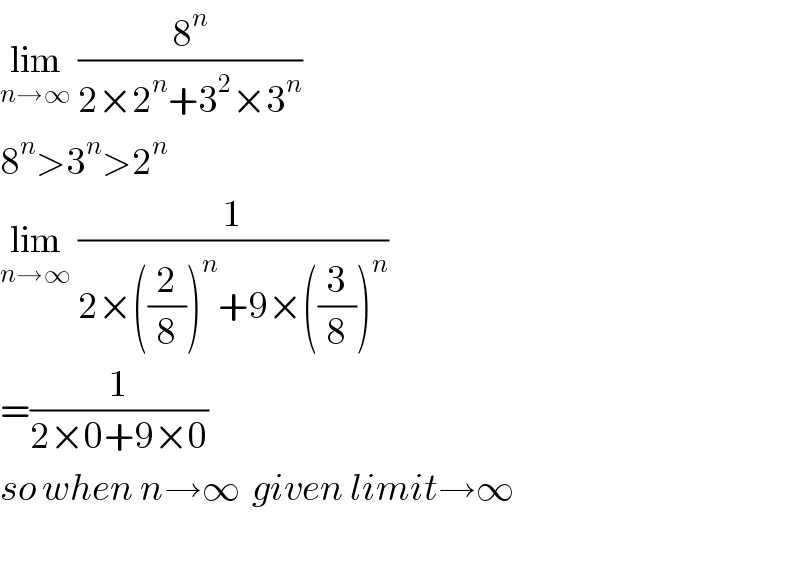
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{8}^{{n}} }{\mathrm{2}×\mathrm{2}^{{n}} +\mathrm{3}^{\mathrm{2}} ×\mathrm{3}^{{n}} } \\ $$$$\mathrm{8}^{{n}} >\mathrm{3}^{{n}} >\mathrm{2}^{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}×\left(\frac{\mathrm{2}}{\mathrm{8}}\right)^{{n}} +\mathrm{9}×\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{0}+\mathrm{9}×\mathrm{0}} \\ $$$${so}\:{when}\:{n}\rightarrow\infty\:\:{given}\:{limit}\rightarrow\infty \\ $$$$ \\ $$
Commented by Mikael_Marshall last updated on 13/Apr/19

$${thanks}\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19

$${most}\:{welcome} \\ $$
