Question Number 127961 by bramlexs22 last updated on 03/Jan/21
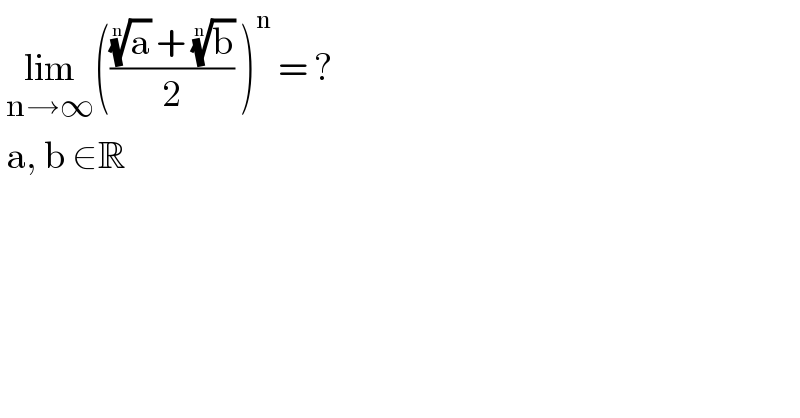
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt[{\mathrm{n}}]{\mathrm{a}}\:+\:\sqrt[{\mathrm{n}}]{\mathrm{b}}}{\mathrm{2}}\:\right)^{\mathrm{n}} \:=\:?\: \\ $$$$\:\mathrm{a},\:\mathrm{b}\:\in\mathbb{R}\: \\ $$
Answered by liberty last updated on 03/Jan/21
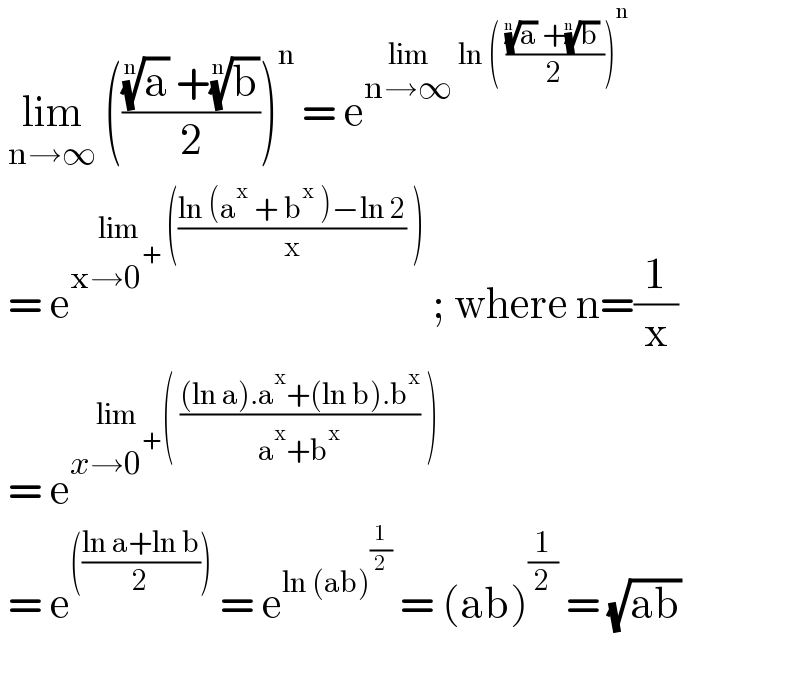
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\sqrt[{\mathrm{n}}]{\mathrm{a}}\:+\sqrt[{\mathrm{n}}]{\mathrm{b}}}{\mathrm{2}}\right)^{\mathrm{n}} \:=\:\mathrm{e}^{\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ln}\:\left(\:\frac{\sqrt[{\mathrm{n}}]{\mathrm{a}}\:+\sqrt[{\mathrm{n}}]{\mathrm{b}}\:}{\mathrm{2}}\right)^{\mathrm{n}} } \\ $$$$\:=\:\mathrm{e}^{\underset{\mathrm{x}\rightarrow\mathrm{0}^{+\:} } {\mathrm{lim}}\left(\frac{\mathrm{ln}\:\left(\mathrm{a}^{\mathrm{x}} \:+\:\mathrm{b}^{\mathrm{x}} \:\right)−\mathrm{ln}\:\mathrm{2}}{\mathrm{x}}\:\right)} \:;\:\mathrm{where}\:\mathrm{n}=\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\:\frac{\left(\mathrm{ln}\:\mathrm{a}\right).\mathrm{a}^{\mathrm{x}} +\left(\mathrm{ln}\:\mathrm{b}\right).\mathrm{b}^{\mathrm{x}} }{\mathrm{a}^{\mathrm{x}} +\mathrm{b}^{\mathrm{x}} }\:\right)} \\ $$$$\:=\:\mathrm{e}^{\left(\frac{\mathrm{ln}\:\mathrm{a}+\mathrm{ln}\:\mathrm{b}}{\mathrm{2}}\right)} \:=\:\mathrm{e}^{\mathrm{ln}\:\left(\mathrm{ab}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \:=\:\left(\mathrm{ab}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\sqrt{\mathrm{ab}}\: \\ $$$$ \\ $$
