Question Number 146155 by mnjuly1970 last updated on 11/Jul/21

$$ \\ $$$$\:\:\:\:\:\:{lim}_{{n}\rightarrow\infty} \:\left({Arcsin}\left({x}\right)\right)^{\:{n}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\:{x}\:\in\:?\: \\ $$$$\:\:\:\:\:\:{Q}\::\:{mr}\:{liberty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by mathmax by abdo last updated on 11/Jul/21
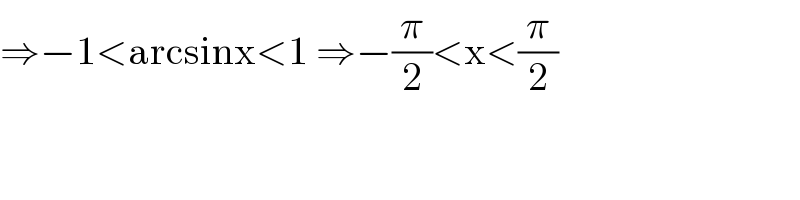
$$\Rightarrow−\mathrm{1}<\mathrm{arcsinx}<\mathrm{1}\:\Rightarrow−\frac{\pi}{\mathrm{2}}<\mathrm{x}<\frac{\pi}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 12/Jul/21
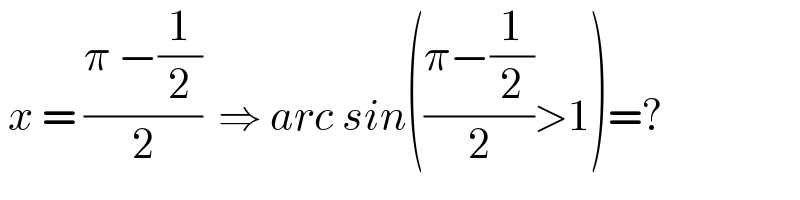
$$\:{x}\:=\:\frac{\pi\:−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}\:\:\Rightarrow\:{arc}\:{sin}\left(\frac{\pi−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}>\mathrm{1}\right)=? \\ $$
