Menu Close

lim-n-cos-x-n-dx-where-n-2k-k-N-k-0-

Tinku Tara 0 Comments
Pin




Question Number 100368 by bemath last updated on 26/Jun/20
lim_(n→∞) ∫_(−∞) ^∞ cos (x^n ) dx =? where n=2k, k∈N, k≠0
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\int_{−\infty} ^{\infty} \mathrm{cos}\:\left({x}^{{n}} \right)\:{dx}\:=? \\ $$$${where}\:{n}=\mathrm{2}{k},\:{k}\in\mathbb{N},\:{k}\neq\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 26/Jun/20
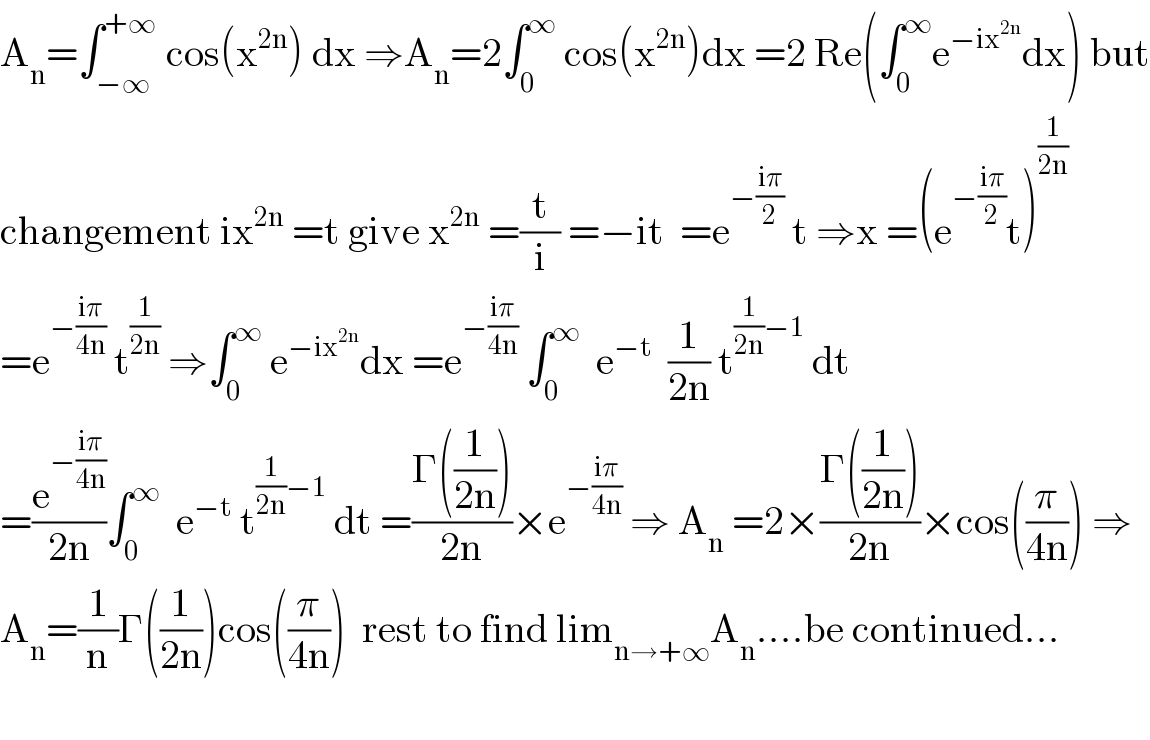
A_n =∫_(−∞) ^(+∞) cos(x^(2n) ) dx ⇒A_n =2∫_0 ^∞ cos(x^(2n) )dx =2 Re(∫_0 ^∞ e^(−ix^(2n) ) dx) but changement ix^(2n) =t give x^(2n) =(t/i) =−it =e^(−((iπ)/2)) t ⇒x =(e^(−((iπ)/2)) t)^(1/(2n)) =e^(−((iπ)/(4n))) t^(1/(2n)) ⇒∫_0 ^∞ e^(−ix^(2n) ) dx =e^(−((iπ)/(4n))) ∫_0 ^∞ e^(−t) (1/(2n)) t^((1/(2n))−1) dt =(e^(−((iπ)/(4n))) /(2n))∫_0 ^∞ e^(−t) t^((1/(2n))−1) dt =((Γ((1/(2n))))/(2n))×e^(−((iπ)/(4n))) ⇒ A_n =2×((Γ((1/(2n))))/(2n))×cos((π/(4n))) ⇒ A_n =(1/n)Γ((1/(2n)))cos((π/(4n))) rest to find lim_(n→+∞) A_n ....be continued...
$$\mathrm{A}_{\mathrm{n}} =\int_{−\infty} ^{+\infty} \:\mathrm{cos}\left(\mathrm{x}^{\mathrm{2n}} \right)\:\mathrm{dx}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx}\:=\mathrm{2}\:\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{ix}^{\mathrm{2n}} } \mathrm{dx}\right)\:\mathrm{but} \\ $$$$\mathrm{changement}\:\mathrm{ix}^{\mathrm{2n}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}^{\mathrm{2n}} \:=\frac{\mathrm{t}}{\mathrm{i}}\:=−\mathrm{it}\:\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \:\mathrm{t}\:\Rightarrow\mathrm{x}\:=\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{2n}}} \\ $$$$=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4n}}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}} \:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{ix}^{\mathrm{2n}} } \mathrm{dx}\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4n}}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{2n}}\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4n}}} }{\mathrm{2n}}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}\right)}{\mathrm{2n}}×\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4n}}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} \:=\mathrm{2}×\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}\right)}{\mathrm{2n}}×\mathrm{cos}\left(\frac{\pi}{\mathrm{4n}}\right)\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{4n}}\right)\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} ….\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 26/Jun/20
thnk you sir.
$$\mathrm{thnk}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Ar Brandon last updated on 26/Jun/20
wow, cool !
Commented by maths mind last updated on 26/Jun/20
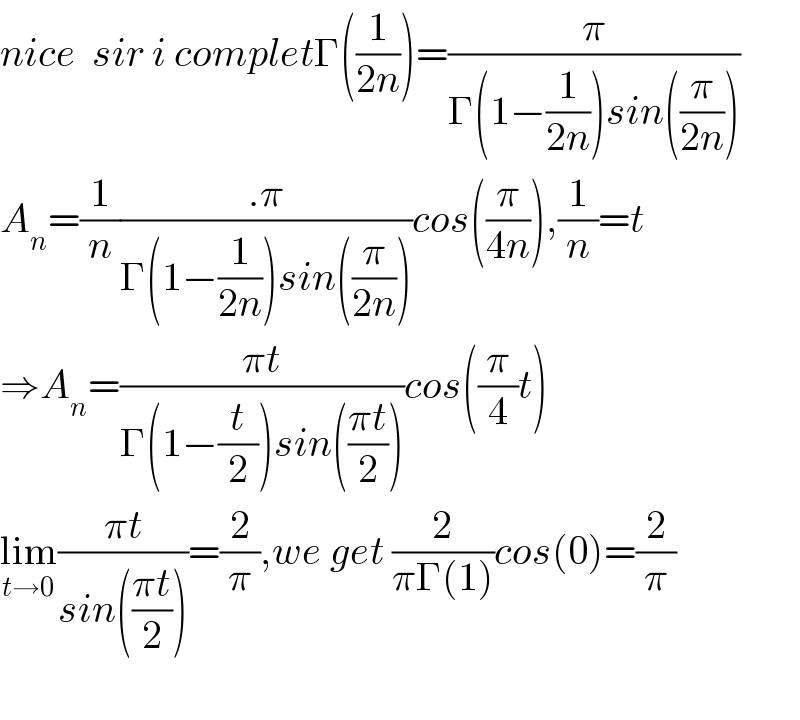
nice sir i completΓ((1/(2n)))=(π/(Γ(1−(1/(2n)))sin((π/(2n))))) A_n =(1/n)((.π)/(Γ(1−(1/(2n)))sin((π/(2n)))))cos((π/(4n))),(1/n)=t ⇒A_n =((πt)/(Γ(1−(t/2))sin(((πt)/2))))cos((π/4)t) lim_(t→0) ((πt)/(sin(((πt)/2))))=(2/π),we get (2/(πΓ(1)))cos(0)=(2/π)
$${nice}\:\:{sir}\:{i}\:{complet}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)=\frac{\pi}{\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right){sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)} \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{{n}}\frac{.\pi}{\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right){sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right),\frac{\mathrm{1}}{{n}}={t} \\ $$$$\Rightarrow{A}_{{n}} =\frac{\pi{t}}{\Gamma\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right){sin}\left(\frac{\pi{t}}{\mathrm{2}}\right)}{cos}\left(\frac{\pi}{\mathrm{4}}{t}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi{t}}{{sin}\left(\frac{\pi{t}}{\mathrm{2}}\right)}=\frac{\mathrm{2}}{\pi},{we}\:{get}\:\frac{\mathrm{2}}{\pi\Gamma\left(\mathrm{1}\right)}{cos}\left(\mathrm{0}\right)=\frac{\mathrm{2}}{\pi} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 27/Jun/20
Are you talking to yourself, Sir ?��
Commented by mathmax by abdo last updated on 27/Jun/20
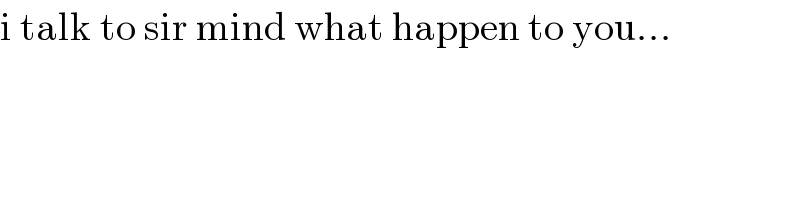
i talk to sir mind what happen to you...
$$\mathrm{i}\:\mathrm{talk}\:\mathrm{to}\:\mathrm{sir}\:\mathrm{mind}\:\mathrm{what}\:\mathrm{happen}\:\mathrm{to}\:\mathrm{you}… \\ $$
Commented by Ar Brandon last updated on 27/Jun/20
Oh sorry ! �� I just feel you both are alike. ����
Commented by maths mind last updated on 27/Jun/20
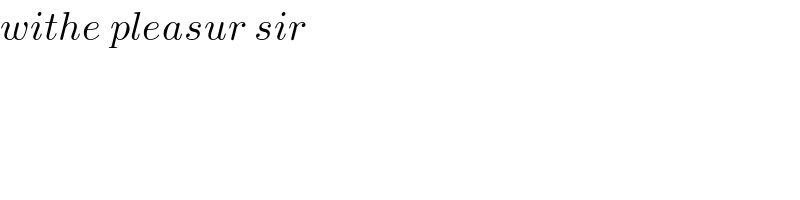
withe pleasur sir
$${withe}\:{pleasur}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *