Question Number 34951 by rahul 19 last updated on 13/May/18
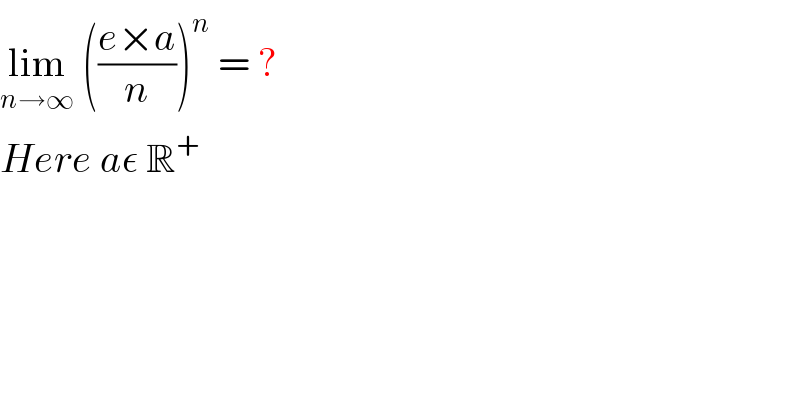
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{e}×{a}}{{n}}\right)^{{n}} \:=\:?\: \\ $$$${Here}\:{a}\epsilon\:\mathbb{R}^{+} \\ $$
Answered by MJS last updated on 14/May/18
![ae=p∈R^+ lim_(n→∞) (p^n /n^n )=L L=lim_(n→∞) (p^n /n^n )=lim_(n→∞) (((d/dn)[p^n ])/((d/dn)[n^n ]))=lim_(n→∞) ((ln(p)×p^n )/((1+ln(n))×n^n ))= =L×lim_(n→∞) ((ln(p))/(1+ln(n)))=L×0=0](https://www.tinkutara.com/question/Q35042.png)
$${a}\mathrm{e}={p}\in\mathbb{R}^{+} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{p}^{{n}} }{{n}^{{n}} }={L} \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{p}^{{n}} }{{n}^{{n}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\frac{{d}}{{dn}}\left[{p}^{{n}} \right]}{\frac{{d}}{{dn}}\left[{n}^{{n}} \right]}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\left({p}\right)×{p}^{{n}} }{\left(\mathrm{1}+\mathrm{ln}\left({n}\right)\right)×{n}^{{n}} }= \\ $$$$={L}×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\left({p}\right)}{\mathrm{1}+\mathrm{ln}\left({n}\right)}={L}×\mathrm{0}=\mathrm{0} \\ $$
