Question Number 124268 by bramlexs22 last updated on 02/Dec/20
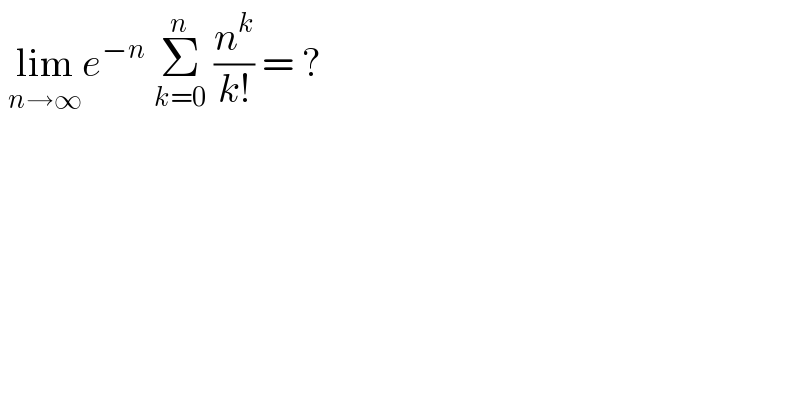
$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{e}^{−{n}} \:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{{n}^{{k}} }{{k}!}\:=\:? \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
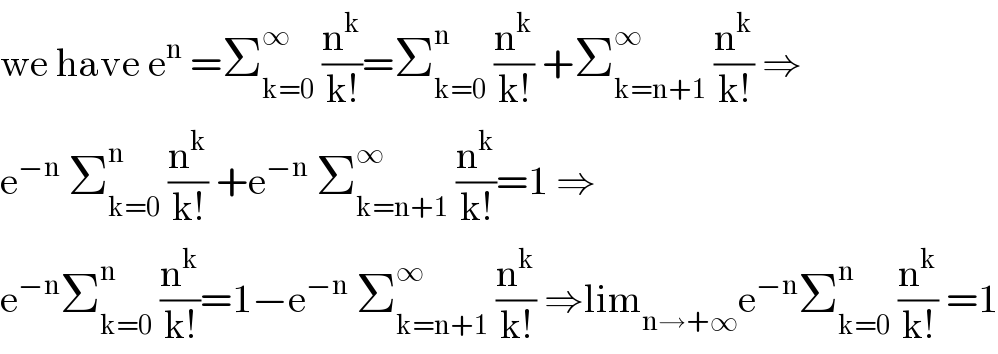
$$\mathrm{we}\:\mathrm{have}\:\mathrm{e}^{\mathrm{n}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}\:+\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}\:\Rightarrow \\ $$$$\mathrm{e}^{−\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}\:+\mathrm{e}^{−\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{e}^{−\mathrm{n}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}=\mathrm{1}−\mathrm{e}^{−\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{e}^{−\mathrm{n}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{n}^{\mathrm{k}} }{\mathrm{k}!}\:=\mathrm{1} \\ $$
