Menu Close

lim-n-k-0-2n-2-k-cos-k-n-

Tinku Tara 0 Comments
Pin




Question Number 166572 by qaz last updated on 22/Feb/22
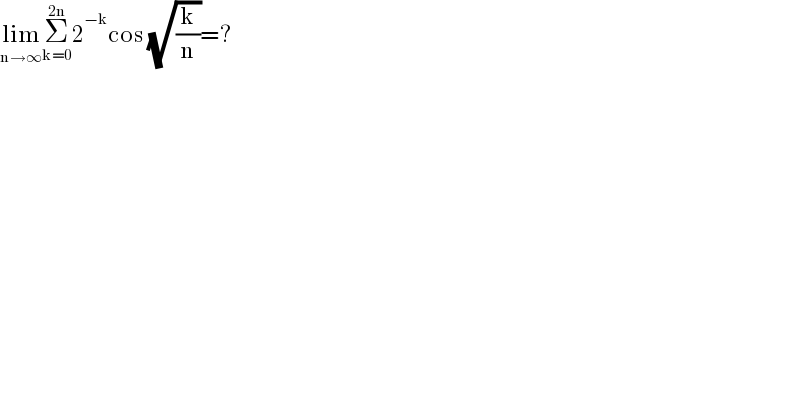
lim_(n→∞) Σ_(k=0) ^(2n) 2^(−k) cos (√(k/n))=?
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\mathrm{2}^{−\mathrm{k}} \mathrm{cos}\:\sqrt{\frac{\mathrm{k}}{\mathrm{n}}}=? \\ $$
Answered by alephzero last updated on 23/Feb/22
lim_(n→∞) Σ_(k=0) ^(2n) 2^(−k) cos (√(k/n)) = ? If n→∞ ⇒ (k/n)→0 ∧ 2n→∞ ⇒ Σ_(k=0) ^∞ 2^(−k) cos (√(k/n)) = = Σ_(k=0) ^∞ 2^(−k) cos (√(0 ))= Σ_(k=0) ^∞ 2^(−k) = = Σ_(k=0) ^∞ (1/2^k ) = 1 + ξ(2) = 1 + (1/(2−1)) = = 1 + 1 = 2 ξ(s) = Σ_(k=1) ^∞ (1/s^k ) is my function. One day I was studying convergness of this series. I noticed, that ξ(s) = (1/(s−1)) I cheked this with Wolphram Alpha. It was right. So, this function reveals that (0/0) = −1 (this is weird indeed)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\mathrm{2}^{−{k}} \:\mathrm{cos}\:\sqrt{\frac{{k}}{{n}}}\:=\:? \\ $$$$\mathrm{If}\:{n}\rightarrow\infty\:\Rightarrow\:\frac{{k}}{{n}}\rightarrow\mathrm{0}\:\wedge\:\mathrm{2}{n}\rightarrow\infty \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{2}^{−{k}} \:\mathrm{cos}\:\sqrt{\frac{{k}}{{n}}}\:= \\ $$$$=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{2}^{−{k}} \:\mathrm{cos}\:\sqrt{\mathrm{0}\:}=\:\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{2}^{−{k}} \:= \\ $$$$=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\:=\:\:\mathrm{1}\:+\:\xi\left(\mathrm{2}\right)\:=\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}\:= \\ $$$$=\:\mathrm{1}\:+\:\mathrm{1}\:=\:\mathrm{2} \\ $$$$\xi\left({s}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}^{{k}} }\:\mathrm{is}\:\mathrm{my}\:\mathrm{function}. \\ $$$$\mathrm{One}\:\mathrm{day}\:\mathrm{I}\:\mathrm{was}\:\mathrm{studying}\:\mathrm{convergness} \\ $$$$\mathrm{of}\:\mathrm{this}\:\mathrm{series}.\:\mathrm{I}\:\mathrm{noticed},\:\mathrm{that} \\ $$$$\xi\left({s}\right)\:=\:\frac{\mathrm{1}}{{s}−\mathrm{1}} \\ $$$$\mathrm{I}\:\mathrm{cheked}\:\mathrm{this}\:\mathrm{with}\:\mathrm{Wolphram} \\ $$$$\mathrm{Alpha}.\:\:\mathrm{It}\:\mathrm{was}\:\mathrm{right}.\:\mathrm{So},\:\mathrm{this} \\ $$$$\mathrm{function}\:\mathrm{reveals}\:\mathrm{that}\:\frac{\mathrm{0}}{\mathrm{0}}\:=\:−\mathrm{1} \\ $$$$\left(\mathrm{this}\:\mathrm{is}\:\mathrm{weird}\:\mathrm{indeed}\right) \\ $$
Commented by MJS_new last updated on 22/Feb/22
(0/0) is not defined ⇒ (0/0)=−1 is wrong but you can find limits of the form L=lim_(x→r) ((f(x))/(g(x))) with f(r)=g(r)=0 and any real value of L. this is not a proof for (0/0)=L∈R (because L can be any number we would get i.e. (0/0)=−1=1=π^2 =(√(37))e ...×)
$$\frac{\mathrm{0}}{\mathrm{0}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\Rightarrow\:\frac{\mathrm{0}}{\mathrm{0}}=−\mathrm{1}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{but}\:\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:\mathrm{limits}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$${L}=\underset{{x}\rightarrow{r}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\:\mathrm{with}\:{f}\left({r}\right)={g}\left({r}\right)=\mathrm{0}\:\mathrm{and}\:\mathrm{any} \\ $$$$\mathrm{real}\:\mathrm{value}\:\mathrm{of}\:{L}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{for} \\ $$$$\frac{\mathrm{0}}{\mathrm{0}}={L}\in\mathbb{R}\:\left(\mathrm{because}\:{L}\:\mathrm{can}\:\mathrm{be}\:\mathrm{any}\:\mathrm{number}\:\mathrm{we}\right. \\ $$$$\left.\mathrm{would}\:\mathrm{get}\:\mathrm{i}.\mathrm{e}.\:\frac{\mathrm{0}}{\mathrm{0}}=−\mathrm{1}=\mathrm{1}=\pi^{\mathrm{2}} =\sqrt{\mathrm{37}}\mathrm{e}\:…×\right) \\ $$
Answered by Mathspace last updated on 22/Feb/22
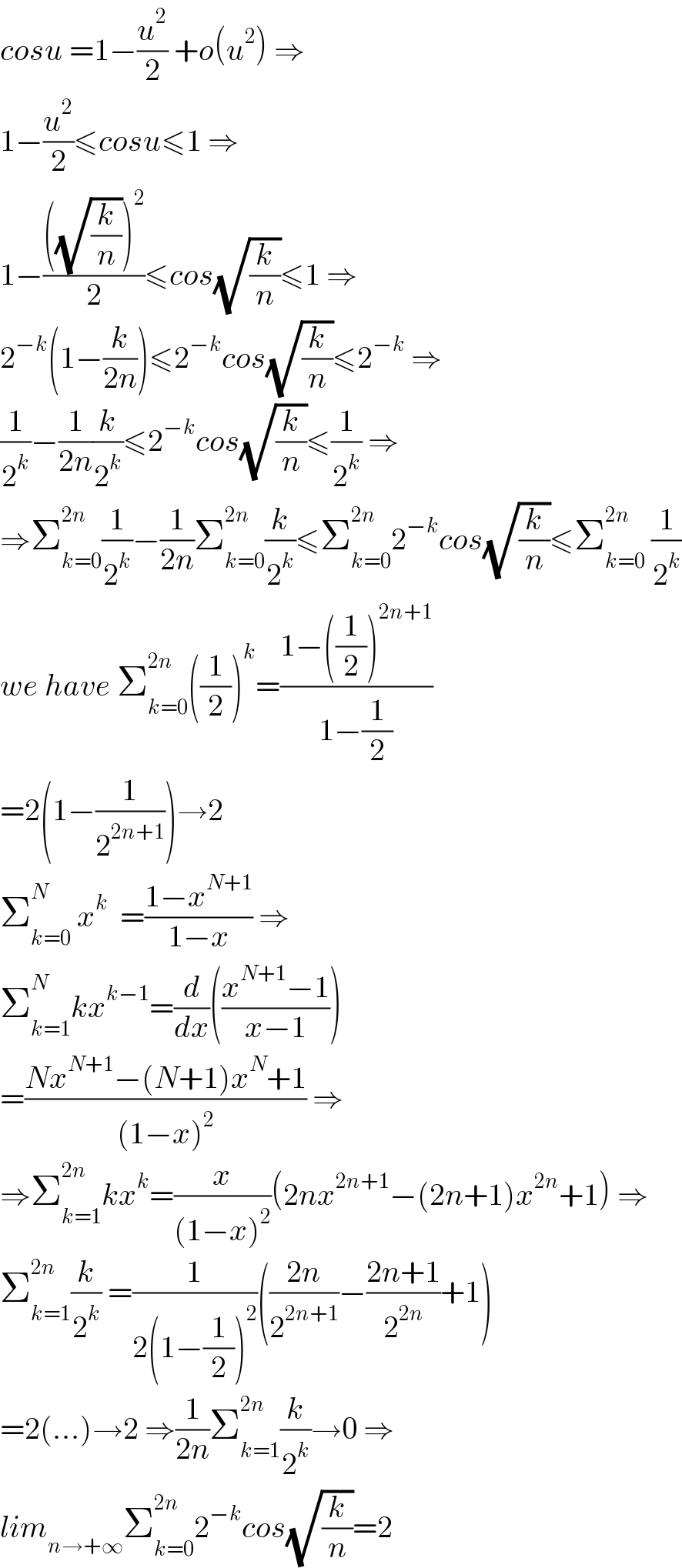
cosu =1−(u^2 /2) +o(u^2 ) ⇒ 1−(u^2 /2)≤cosu≤1 ⇒ 1−((((√(k/n)))^2 )/2)≤cos(√(k/n))≤1 ⇒ 2^(−k) (1−(k/(2n)))≤2^(−k) cos(√(k/n))≤2^(−k) ⇒ (1/2^k )−(1/(2n))(k/2^k )≤2^(−k) cos(√(k/n))≤(1/2^k ) ⇒ ⇒Σ_(k=0) ^(2n) (1/2^k )−(1/(2n))Σ_(k=0) ^(2n) (k/2^k )≤Σ_(k=0) ^(2n) 2^(−k) cos(√(k/n))≤Σ_(k=0) ^(2n) (1/2^k ) we have Σ_(k=0) ^(2n ) ((1/2))^k =((1−((1/2))^(2n+1) )/(1−(1/2))) =2(1−(1/2^(2n+1) ))→2 Σ_(k=0) ^N x^k =((1−x^(N+1) )/(1−x)) ⇒ Σ_(k=1) ^N kx^(k−1) =(d/dx)(((x^(N+1) −1)/(x−1))) =((Nx^(N+1) −(N+1)x^N +1)/((1−x)^2 )) ⇒ ⇒Σ_(k=1) ^(2n) kx^k =(x/((1−x)^2 ))(2nx^(2n+1) −(2n+1)x^(2n) +1) ⇒ Σ_(k=1) ^(2n) (k/2^k ) =(1/(2(1−(1/2))^2 ))(((2n)/2^(2n+1) )−((2n+1)/2^(2n) )+1) =2(...)→2 ⇒(1/(2n))Σ_(k=1) ^(2n) (k/2^k )→0 ⇒ lim_(n→+∞) Σ_(k=0) ^(2n) 2^(−k) cos(√(k/n))=2
$${cosu}\:=\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\leqslant{cosu}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{1}−\frac{\left(\sqrt{\frac{{k}}{{n}}}\right)^{\mathrm{2}} }{\mathrm{2}}\leqslant{cos}\sqrt{\frac{{k}}{{n}}}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{2}^{−{k}} \left(\mathrm{1}−\frac{{k}}{\mathrm{2}{n}}\right)\leqslant\mathrm{2}^{−{k}} {cos}\sqrt{\frac{{k}}{{n}}}\leqslant\mathrm{2}^{−{k}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{{k}} }−\frac{\mathrm{1}}{\mathrm{2}{n}}\frac{{k}}{\mathrm{2}^{{k}} }\leqslant\mathrm{2}^{−{k}} {cos}\sqrt{\frac{{k}}{{n}}}\leqslant\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\:\Rightarrow \\ $$$$\Rightarrow\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \frac{\mathrm{1}}{\mathrm{2}^{{k}} }−\frac{\mathrm{1}}{\mathrm{2}{n}}\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \frac{{k}}{\mathrm{2}^{{k}} }\leqslant\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \mathrm{2}^{−{k}} {cos}\sqrt{\frac{{k}}{{n}}}\leqslant\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$${we}\:{have}\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}\:} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}} =\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\right)\rightarrow\mathrm{2} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{N}} \:{x}^{{k}} \:\:=\frac{\mathrm{1}−{x}^{{N}+\mathrm{1}} }{\mathrm{1}−{x}}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{N}} {kx}^{{k}−\mathrm{1}} =\frac{{d}}{{dx}}\left(\frac{{x}^{{N}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$=\frac{{Nx}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\Rightarrow\sum_{{k}=\mathrm{1}} ^{\mathrm{2}{n}} {kx}^{{k}} =\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\left(\mathrm{2}{nx}^{\mathrm{2}{n}+\mathrm{1}} −\left(\mathrm{2}{n}+\mathrm{1}\right){x}^{\mathrm{2}{n}} +\mathrm{1}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{2}{n}} \frac{{k}}{\mathrm{2}^{{k}} }\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\left(\frac{\mathrm{2}{n}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }−\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} }+\mathrm{1}\right) \\ $$$$=\mathrm{2}\left(…\right)\rightarrow\mathrm{2}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{n}}\sum_{{k}=\mathrm{1}} ^{\mathrm{2}{n}} \frac{{k}}{\mathrm{2}^{{k}} }\rightarrow\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \mathrm{2}^{−{k}} {cos}\sqrt{\frac{{k}}{{n}}}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *