Menu Close

lim-n-k-0-2n-k-k-n-2-

Tinku Tara 0 Comments
Pin




Question Number 99697 by Ar Brandon last updated on 22/Jun/20
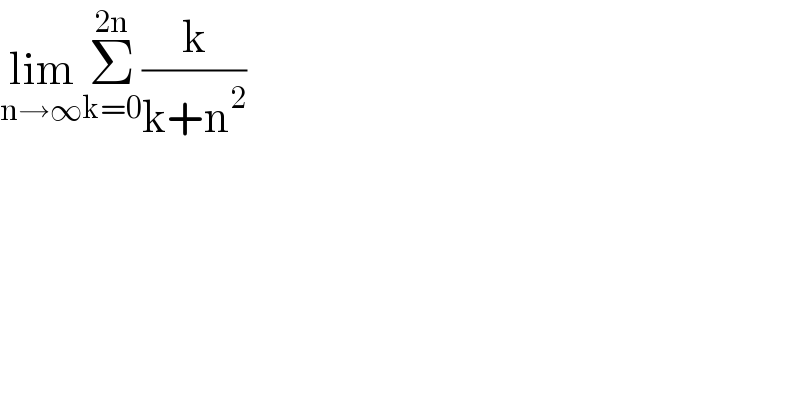
lim_(n→∞) Σ_(k=0) ^(2n) (k/(k+n^2 ))
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} } \\ $$
Commented by MWSuSon last updated on 22/Jun/20
just dropping a comment so that I'll get notified when someone solves it. if only the k in the denominator was k^2��
Answered by Ar Brandon last updated on 23/Jun/20
l=limΣ_(k=0) ^(2n) (k/(k+n^2 )) 0≤k≤2n⇒n^2 ≤k+n^2 ≤2n+n^2 ⇒(1/(2n+n^2 ))≤(1/(k+n^2 ))≤(1/n^2 ) ⇒(k/(2n+n^2 ))≤(k/(k+n^2 ))≤(k/n^2 )⇒Σ_(k=0) ^(2n) (k/(2n+n^2 ))≤Σ_(k=0) ^(2n) (k/(k+n^2 ))≤Σ_(k=0) ^(2n) (k/n^2 ) ⇒((n(2n+1))/(2n+n^2 ))≤Σ_(k=0) ^(2n) (k/(k+n^2 ))≤((n(2n+1))/n^2 )⇒((2+(1/n))/(1+(2/n)))≤Σ_(k=0) ^(2n) (k/(k+n^2 ))≤((2+(1/n))/1) ⇒2≤limΣ_(k=0) ^(2n) (k/(k+n^2 ))≤2⇒limΣ_(k=0) ^(2n) (k/(k+n^2 ))=2
$${l}=\mathrm{lim}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} } \\ $$$$\mathrm{0}\leqslant\mathrm{k}\leqslant\mathrm{2n}\Rightarrow\mathrm{n}^{\mathrm{2}} \leqslant\mathrm{k}+\mathrm{n}^{\mathrm{2}} \leqslant\mathrm{2n}+\mathrm{n}^{\mathrm{2}} \Rightarrow\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{k}}{\mathrm{2n}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\Rightarrow\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{2n}+\mathrm{n}^{\mathrm{2}} }\leqslant\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{n}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{2n}+\mathrm{n}^{\mathrm{2}} }\leqslant\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{n}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{n}^{\mathrm{2}} }\Rightarrow\frac{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}}\leqslant\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}\leqslant\mathrm{lim}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }\leqslant\mathrm{2}\Rightarrow\mathrm{lim}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{n}^{\mathrm{2}} }=\mathrm{2} \\ $$
Answered by Ar Brandon last updated on 22/Jun/20
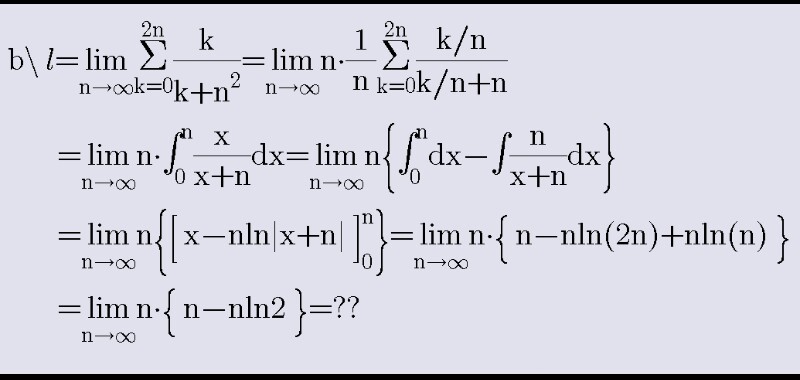
Commented by Ar Brandon last updated on 22/Jun/20
I got this. Am I right ?

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *