Question Number 127454 by snipers237 last updated on 29/Dec/20
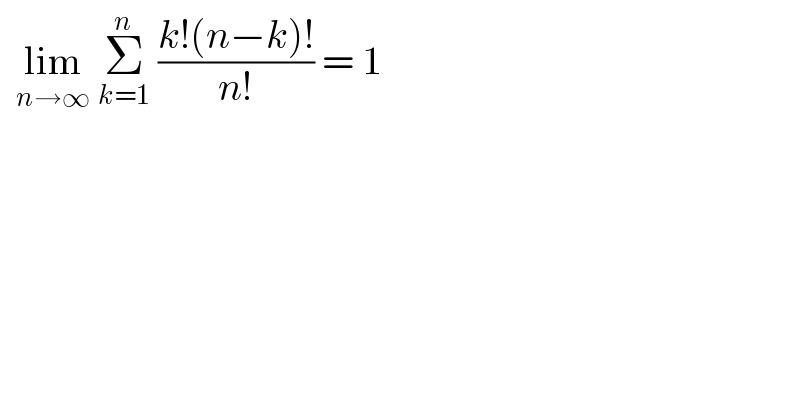
$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{k}!\left({n}−{k}\right)!}{{n}!}\:=\:\mathrm{1} \\ $$
Answered by Ar Brandon last updated on 29/Dec/20
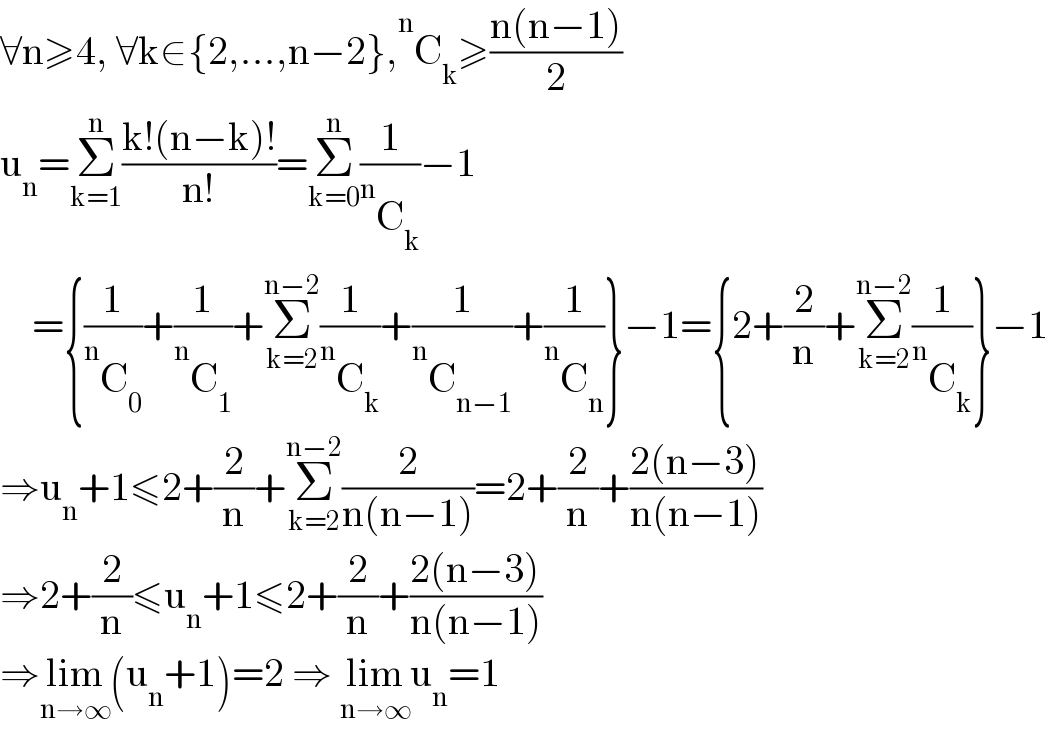
$$\forall\mathrm{n}\geqslant\mathrm{4},\:\forall\mathrm{k}\in\left\{\mathrm{2},…,\mathrm{n}−\mathrm{2}\right\},\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{k}} \geqslant\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}{\mathrm{n}!}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{k}} }−\mathrm{1} \\ $$$$\:\:\:\:=\left\{\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{0}} }+\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{1}} }+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}−\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{k}} }+\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{n}} }\right\}−\mathrm{1}=\left\{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{n}}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}−\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{k}} }\right\}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} +\mathrm{1}\leqslant\mathrm{2}+\frac{\mathrm{2}}{\mathrm{n}}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}−\mathrm{2}} {\sum}}\frac{\mathrm{2}}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}=\mathrm{2}+\frac{\mathrm{2}}{\mathrm{n}}+\frac{\mathrm{2}\left(\mathrm{n}−\mathrm{3}\right)}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{2}+\frac{\mathrm{2}}{\mathrm{n}}\leqslant\mathrm{u}_{\mathrm{n}} +\mathrm{1}\leqslant\mathrm{2}+\frac{\mathrm{2}}{\mathrm{n}}+\frac{\mathrm{2}\left(\mathrm{n}−\mathrm{3}\right)}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)} \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{u}_{\mathrm{n}} +\mathrm{1}\right)=\mathrm{2}\:\Rightarrow\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}u}_{\mathrm{n}} =\mathrm{1} \\ $$
