Question Number 160384 by qaz last updated on 28/Nov/21
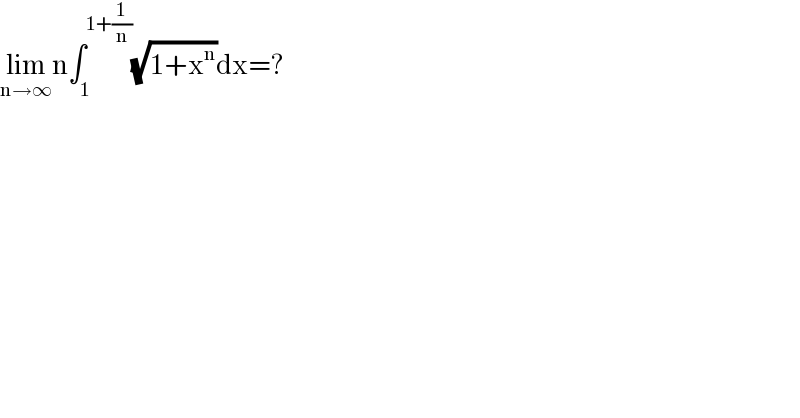
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\int_{\mathrm{1}} ^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}=? \\ $$
Answered by mathmax by abdo last updated on 29/Nov/21
![A_n =n∫_1 ^(1+(1/n)) (√(1+x^n ))dx changement x−1=t give A_n =n∫_0 ^(1/n) (√(1+(t+1)^n ))dt =n∫_0 ^(1/n) (√(1+Σ_(k=0) ^n C_n ^k t^k ))dt =n∫_0 ^(1/n) (√(1+1+Σ_(k=1) ^n C_n ^k t^k ))dt (n→∞ ⇒x→1 ⇒t→0) A_n =n∫_0 ^(1/n) (√2)(√(1+(1/2)Σ_(k=1) ^n C_n ^k t^k ))dt ⇒ A_n ∼n∫_0 ^(1/n) (√2)×(1+(1/4)Σ_(k=1) ^n C_n ^k t^k )dt =(√2)+(n/4)(√2)Σ_(k=1) ^n C_n ^k ∫_0 ^(1/n) t^(k ) dt =(√2)+((n(√2))/4) Σ_(k=1) ^n C_n ^k [(1/(k+1))t^(k+1) ]_0 ^(1/n) =(√2)+((n(√2))/4)Σ_(k=1) ^n C_n ^k (1/((k+1)n^(k+1) )) =(√2)+((√2)/4)Σ_(k=1) ^n ((n!)/(k!(n−k)!(k+1)n^(k+1) )) rest to find lim_(n→+∞) Σ ((n!)/(k!(n−k)!(k+1)n^(k+1) ))....be continued...](https://www.tinkutara.com/question/Q160393.png)
$$\mathrm{A}_{\mathrm{n}} =\mathrm{n}\int_{\mathrm{1}} ^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{n}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dt}\:=\mathrm{n}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{t}^{\mathrm{k}} }\mathrm{dt} \\ $$$$=\mathrm{n}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\mathrm{1}+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{t}^{\mathrm{k}} }\mathrm{dt}\:\:\:\:\left(\mathrm{n}\rightarrow\infty\:\Rightarrow\mathrm{x}\rightarrow\mathrm{1}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{n}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{2}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{t}^{\mathrm{k}} }\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} \sim\mathrm{n}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{2}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \right)\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}+\frac{\mathrm{n}}{\mathrm{4}}\sqrt{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{t}^{\mathrm{k}\:} \mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}+\frac{\mathrm{n}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\mathrm{t}^{\mathrm{k}+\mathrm{1}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$=\sqrt{\mathrm{2}}+\frac{\mathrm{n}\sqrt{\mathrm{2}}}{\mathrm{4}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{n}^{\mathrm{k}+\mathrm{1}} } \\ $$$$=\sqrt{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{k}+\mathrm{1}\right)\mathrm{n}^{\mathrm{k}+\mathrm{1}} } \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \Sigma\:\:\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{k}+\mathrm{1}\right)\mathrm{n}^{\mathrm{k}+\mathrm{1}} }….\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by Kamel last updated on 29/Nov/21

Commented by qaz last updated on 30/Nov/21

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}. \\ $$
