Menu Close

lim-n-n-1-3-n-2-1-1-3-2n-2-3n-1-1-2-

Tinku Tara 0 Comments
Pin




Question Number 122866 by bemath last updated on 20/Nov/20
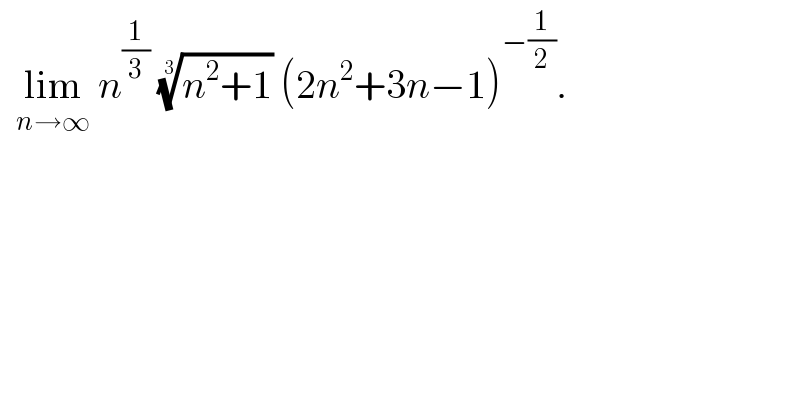
lim_(n→∞) n^(1/3) ((n^2 +1))^(1/3) (2n^2 +3n−1)^(−(1/2)) .
$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} +\mathrm{1}}\:\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} .\: \\ $$
Answered by liberty last updated on 20/Nov/20
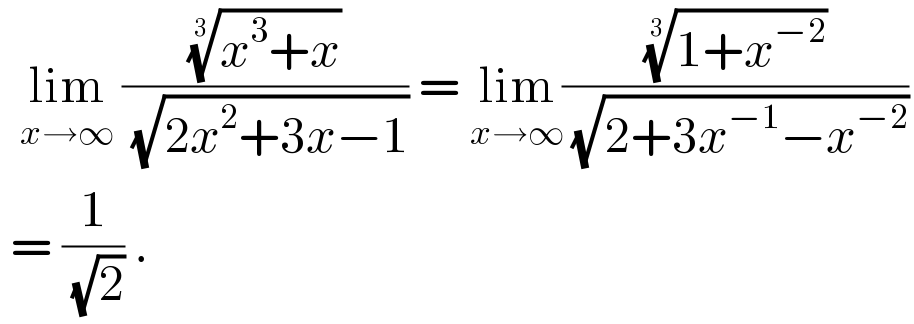
lim_(x→∞) (((x^3 +x))^(1/3) /( (√(2x^2 +3x−1)))) = lim_(x→∞) (((1+x^(−2) ))^(1/3) /( (√(2+3x^(−1) −x^(−2) )))) = (1/( (√2))) .
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1}}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+{x}^{−\mathrm{2}} }}{\:\sqrt{\mathrm{2}+\mathrm{3}{x}^{−\mathrm{1}} −{x}^{−\mathrm{2}} }} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:. \\ $$
Answered by mathmax by abdo last updated on 21/Nov/20
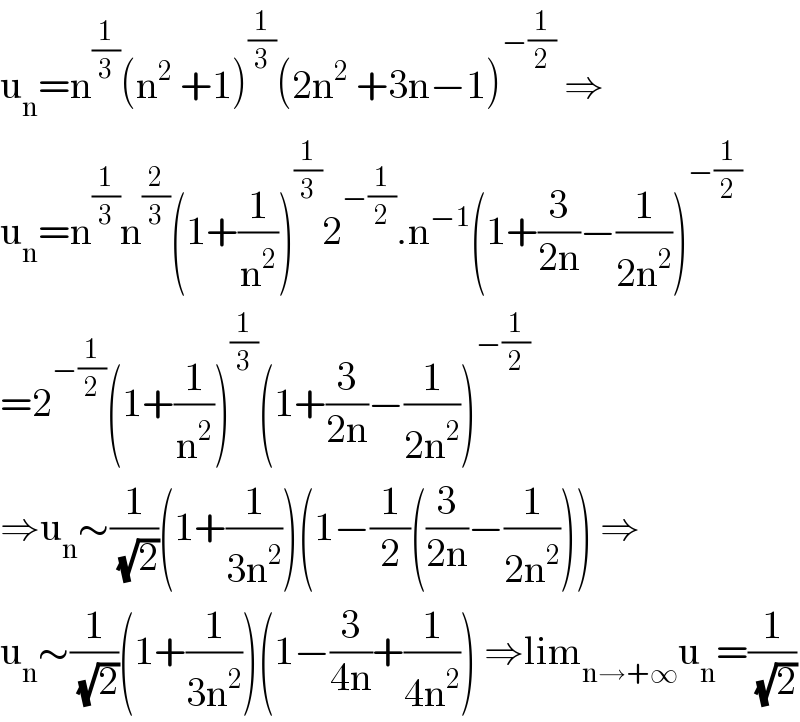
u_n =n^(1/3) (n^2 +1)^(1/3) (2n^2 +3n−1)^(−(1/2)) ⇒ u_n =n^(1/3) n^(2/3) (1+(1/n^2 ))^(1/3) 2^(−(1/2)) .n^(−1) (1+(3/(2n))−(1/(2n^2 )))^(−(1/2)) =2^(−(1/2)) (1+(1/n^2 ))^(1/3) (1+(3/(2n))−(1/(2n^2 )))^(−(1/2)) ⇒u_n ∼(1/( (√2)))(1+(1/(3n^2 )))(1−(1/2)((3/(2n))−(1/(2n^2 )))) ⇒ u_n ∼(1/( (√2)))(1+(1/(3n^2 )))(1−(3/(4n))+(1/(4n^2 ))) ⇒lim_(n→+∞) u_n =(1/( (√2)))
$$\mathrm{u}_{\mathrm{n}} =\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{n}^{\mathrm{2}} \:+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{2n}^{\mathrm{2}} \:+\mathrm{3n}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{n}^{−\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} \sim\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3n}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\right)\right)\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} \sim\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3n}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4n}}+\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *