Question Number 119852 by benjo_mathlover last updated on 27/Oct/20
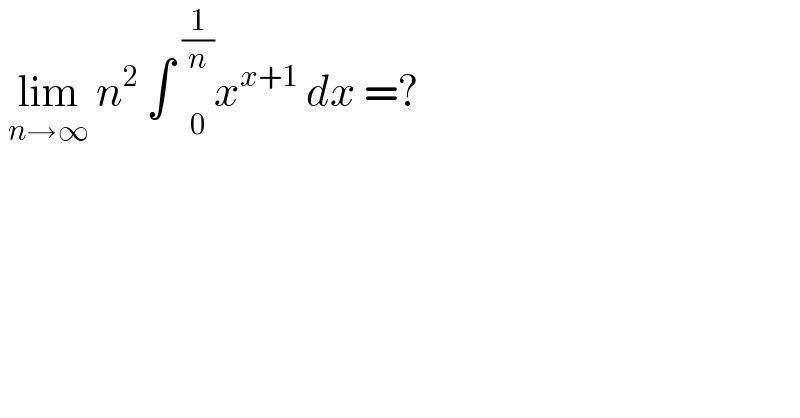
$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{\mathrm{2}} \:\int\:\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{{n}}} {\:}}{x}^{{x}+\mathrm{1}} \:{dx}\:=? \\ $$
Answered by Olaf last updated on 27/Oct/20
![∫_0 ^(1/n) x^(n+1) dx = [(x^(n+2) /(n+2))]_0 ^(1/n) = (1/((n+2)n^(n+2) )) n^2 ∫_0 ^(1/n) x^(n+1) dx = (1/((n+2)n^n )) →_∞ 0](https://www.tinkutara.com/question/Q119864.png)
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} {x}^{{n}+\mathrm{1}} {dx}\:=\:\left[\frac{{x}^{{n}+\mathrm{2}} }{{n}+\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} \:=\:\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right){n}^{{n}+\mathrm{2}} } \\ $$$${n}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} {x}^{{n}+\mathrm{1}} {dx}\:=\:\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right){n}^{{n}} }\:\underset{\infty} {\rightarrow}\:\mathrm{0} \\ $$$$ \\ $$
