Question Number 173734 by mnjuly1970 last updated on 17/Jul/22
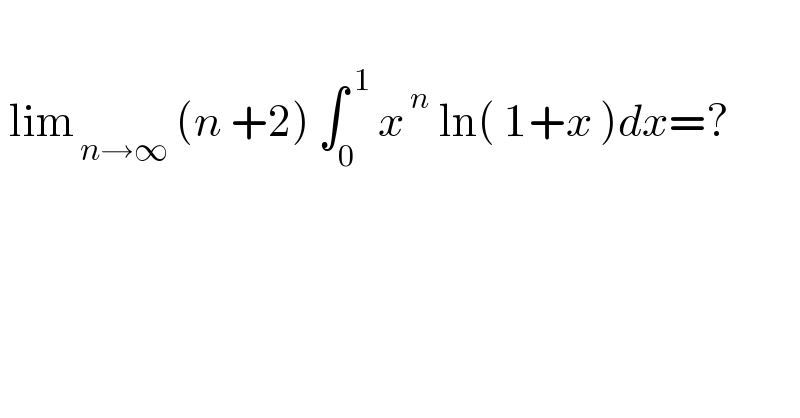
$$ \\ $$$$\:\mathrm{lim}_{\:{n}\rightarrow\infty} \:\left({n}\:+\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:{x}^{\:{n}} \:\mathrm{ln}\left(\:\mathrm{1}+{x}\:\right){dx}=? \\ $$$$ \\ $$
Answered by mindispower last updated on 17/Jul/22
![∫_0 ^1 x^n ln(1+x)dx=I_n =[((x^(n+1) ln(1+x))/(n+1))]_0 ^1 −(1/(n+1))∫_0 ^1 (x^(n+1) /(1+x))dx =((ln(2))/(n+1))−(a_n /(n+1)) (1/2)≤(1/(1+x))≤1,∀x∈[0,1] ⇒(1/(2(n+1)))≤a_n ≤(1/(n+1)) ⇔ −(1/((1+n)^2 ))+((ln(2))/(n+1))≤I_n ≤−(1/(2(1+n)^2 ))+((ln(2))/(n+1)) lim_(n→∞) (n+2)I_n =ln(2)](https://www.tinkutara.com/question/Q173740.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {ln}\left(\mathrm{1}+{x}\right){dx}={I}_{{n}} \\ $$$$=\left[\frac{{x}^{{n}+\mathrm{1}} {ln}\left(\mathrm{1}+{x}\right)}{{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{\mathrm{1}+{x}}{dx} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}}−\frac{{a}_{{n}} }{{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\mathrm{1}+{x}}\leqslant\mathrm{1},\forall{x}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\leqslant{a}_{{n}} \leqslant\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\Leftrightarrow\:\:\:\:−\frac{\mathrm{1}}{\left(\mathrm{1}+{n}\right)^{\mathrm{2}} }+\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}}\leqslant{I}_{{n}} \leqslant−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{n}\right)^{\mathrm{2}} }+\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({n}+\mathrm{2}\right){I}_{{n}} ={ln}\left(\mathrm{2}\right) \\ $$
