Question Number 128422 by Khalmohmmad last updated on 07/Jan/21
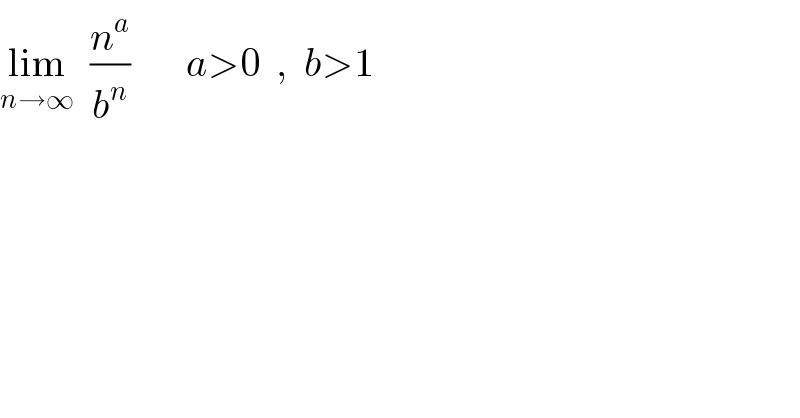
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{{n}^{{a}} }{{b}^{{n}} }\:\:\:\:\:\:\:{a}>\mathrm{0}\:\:,\:\:{b}>\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 07/Jan/21
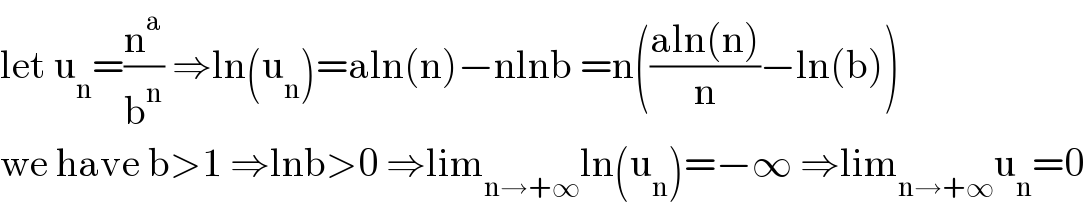
$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{n}^{\mathrm{a}} }{\mathrm{b}^{\mathrm{n}} }\:\Rightarrow\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=\mathrm{aln}\left(\mathrm{n}\right)−\mathrm{nlnb}\:=\mathrm{n}\left(\frac{\mathrm{aln}\left(\mathrm{n}\right)}{\mathrm{n}}−\mathrm{ln}\left(\mathrm{b}\right)\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{b}>\mathrm{1}\:\Rightarrow\mathrm{lnb}>\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=−\infty\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{0} \\ $$
